bitWalk's: 【備忘録】主成分分析～ R ～

主成分分析 (Principal Component Analysis, PCA) は、１観測あたり多数の次元／特徴を含む大規模データセットを分析し、最大限の情報量を保持しながらデータの解釈可能性を高め、多次元データの可視化を可能にする手法としてよく利用されています。形式的には、PCA はデータセットの次元を減少させる統計的手法です。これは、データの変動（の大部分）が、初期データよりも少ない次元で記述できるような新しい座標系にデータを線形変換することにより達成できます。

Wikipedia より引用、翻訳・編集

データ解析で頻繁に主成分分析 (PCA) を利用しています。主成分分析をはじめ、よく使用する機械学習の処理部分などは、いつも過去に使ったスクリプトから必要部分をコピペして使い回してしまっているので、思い違いや間違いがあれば、そのままずっと引きずってしまう可能性があります。ちょっと心配になってきたので、簡単なサンプルを使ってスクリプトを整理しようとしています。

今回は R で主成分分析を扱います。これは、本ブログ記事にまとめた Python / Scikit-Learn における主成分分析のやり方あるいは結果と比較するためです^[1]。

下記の OS 環境で動作確認をしています。

	Fedora Linux 37 Workstation	x86_64
	R	4.2.2

今回は JupyterLab の Notebook 上で動作確認をしています。JupyterLab 上で R を利用するには、本ブログの記事 [2] を参照してください。

最初にプロット関連のモジュールを読み込んでおきます。

library(ggplot2)
library(GGally)

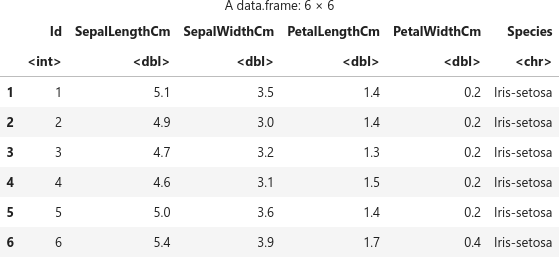
解析用のサンプルデータを読み込みます。解析用のサンプルは有名な Iris のデータセットを使っています。Kaggle のサイトで公開されている CSV データ Iris.csv [3] をダウンロードして使用しています。

filename <- "Iris.csv"
df <- read.csv (filename)
head(df)

複数の変数（説明変数）x とターゲット（目的変数）y のカラムを定義しておきます。

cols.x <- colnames(df)[2:5]
print(cols.x)
col.y <- colnames(df)[6]
print(col.y)

[1] "SepalLengthCm" "SepalWidthCm"  "PetalLengthCm" "PetalWidthCm" 
[1] "Species"

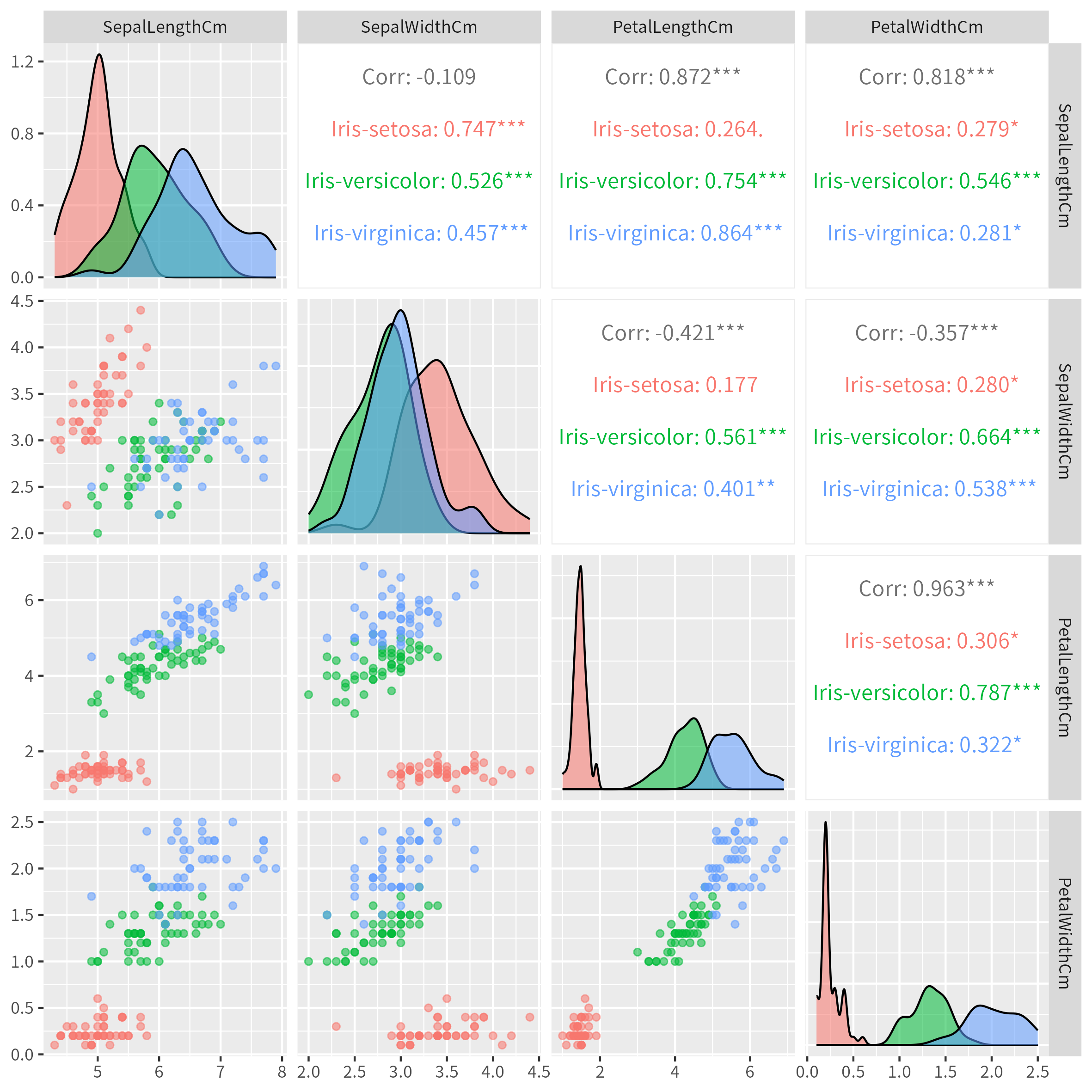
元データ（説明変数）の分布を散布図にして確認しておきます。

p <- ggpairs(
    data = df,
    columns = cols.x,
    mapping = aes(color = Species, alpha = 0.5)
)
ggsave(
    filename = "iris_011_scatter.png", 
    plot = p, 
    width = 20, 
    height = 20, 
    units = "cm"
)
show(p)

主成分分析 (PCA) は、ここでは prcomp で計算します。

pca <- prcomp(df[cols.x], scale. = TRUE)
pca

Standard deviations (1, .., p=4):
[1] 1.7061120 0.9598025 0.3838662 0.1435538

Rotation (n x k) = (4 x 4):
                     PC1         PC2        PC3        PC4
SepalLengthCm  0.5223716 -0.37231836  0.7210168  0.2619956
SepalWidthCm  -0.2633549 -0.92555649 -0.2420329 -0.1241348
PetalLengthCm  0.5812540 -0.02109478 -0.1408923 -0.8011543
PetalWidthCm   0.5656110 -0.06541577 -0.6338014  0.5235463

計算した結果のオブジェクト pca の構造は以下の様になっています。

str(pca)

List of 5
 $ sdev    : num [1:4] 1.706 0.96 0.384 0.144
 $ rotation: num [1:4, 1:4] 0.522 -0.263 0.581 0.566 -0.372 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:4] "SepalLengthCm" "SepalWidthCm" "PetalLengthCm" "PetalWidthCm"
  .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4"
 $ center  : Named num [1:4] 5.84 3.05 3.76 1.2
  ..- attr(*, "names")= chr [1:4] "SepalLengthCm" "SepalWidthCm" "PetalLengthCm" "PetalWidthCm"
 $ scale   : Named num [1:4] 0.828 0.434 1.764 0.763
  ..- attr(*, "names")= chr [1:4] "SepalLengthCm" "SepalWidthCm" "PetalLengthCm" "PetalWidthCm"
 $ x       : num [1:150, 1:4] -2.26 -2.08 -2.36 -2.3 -2.38 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4"
 - attr(*, "class")= chr "prcomp"

pca の summary は次の様になっています。

summary(pca)

mportance of components:
                          PC1    PC2     PC3     PC4
Standard deviation     1.7061 0.9598 0.38387 0.14355
Proportion of Variance 0.7277 0.2303 0.03684 0.00515
Cumulative Proportion  0.7277 0.9580 0.99485 1.00000

上表の３行目の　Cumulative Proportion が、そのまま累積寄与率に使えそうです。summary(pca) の構造を確認します。

s <- summary(pca)
str(s)

List of 6
 $ sdev      : num [1:4] 1.706 0.96 0.384 0.144
 $ rotation  : num [1:4, 1:4] 0.522 -0.263 0.581 0.566 -0.372 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:4] "SepalLengthCm" "SepalWidthCm" "PetalLengthCm" "PetalWidthCm"
  .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4"
 $ center    : Named num [1:4] 5.84 3.05 3.76 1.2
  ..- attr(*, "names")= chr [1:4] "SepalLengthCm" "SepalWidthCm" "PetalLengthCm" "PetalWidthCm"
 $ scale     : Named num [1:4] 0.828 0.434 1.764 0.763
  ..- attr(*, "names")= chr [1:4] "SepalLengthCm" "SepalWidthCm" "PetalLengthCm" "PetalWidthCm"
 $ x         : num [1:150, 1:4] -2.26 -2.08 -2.36 -2.3 -2.38 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4"
 $ importance: num [1:3, 1:4] 1.706 0.728 0.728 0.96 0.23 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:3] "Standard deviation" "Proportion of Variance" "Cumulative Proportion"
  .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4"
 - attr(*, "class")= chr "summary.prcomp"

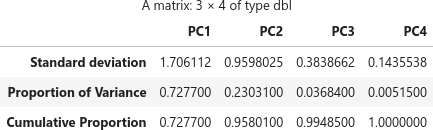
行列 (matrix) s$importance を使えばよさそうです。

s$importance

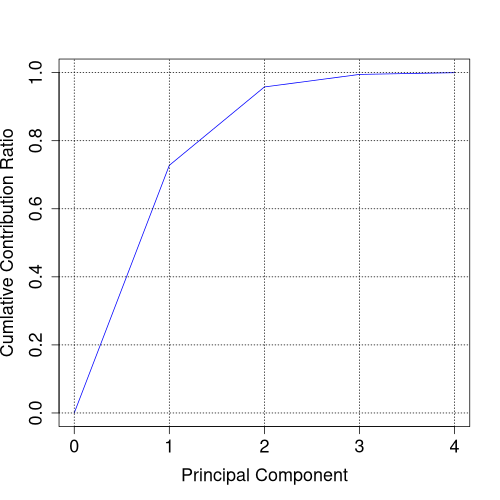
累積寄与率の x 軸を 0 から始めたいので少し加工してプロットします。

contrib <- append(0, s$importance[3, ])
contrib

png("iris_012_contrib.png", width = 500, height = 500)
plot(c(0:4), contrib, type="l", col="blue", xlab="Principal Component", ylab="Cumlative Contribution Ratio", cex.lab=1.5, cex.axis=1.5)
grid(col="black")
dev.off()

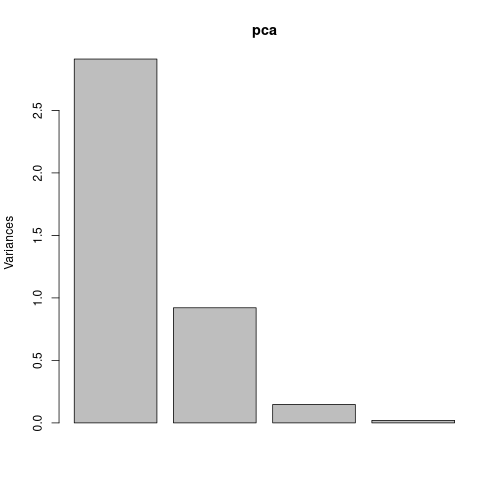
ちなみに、主成分毎の寄与率をプロットするのであれば、screeplot(pca) で簡単にプロットできます。

png("iris_12_screeplot.png", width = 500, height = 500)
screeplot(pca)
dev.off()

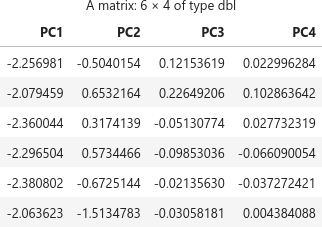
主成分得点のプロットには pca$x を利用します。

head(pca$x)

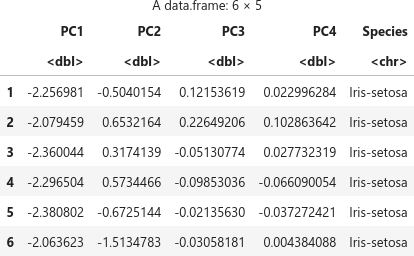
プロット用に pca$x と Species を加えたデータフレーム df.pca を用意します。

df.pca <- as.data.frame(pca$x)
cols.pc <- colnames(df.pca)
print(cols.pc)
df.pca <- cbind(df.pca, df[col.y])
head(df.pca)

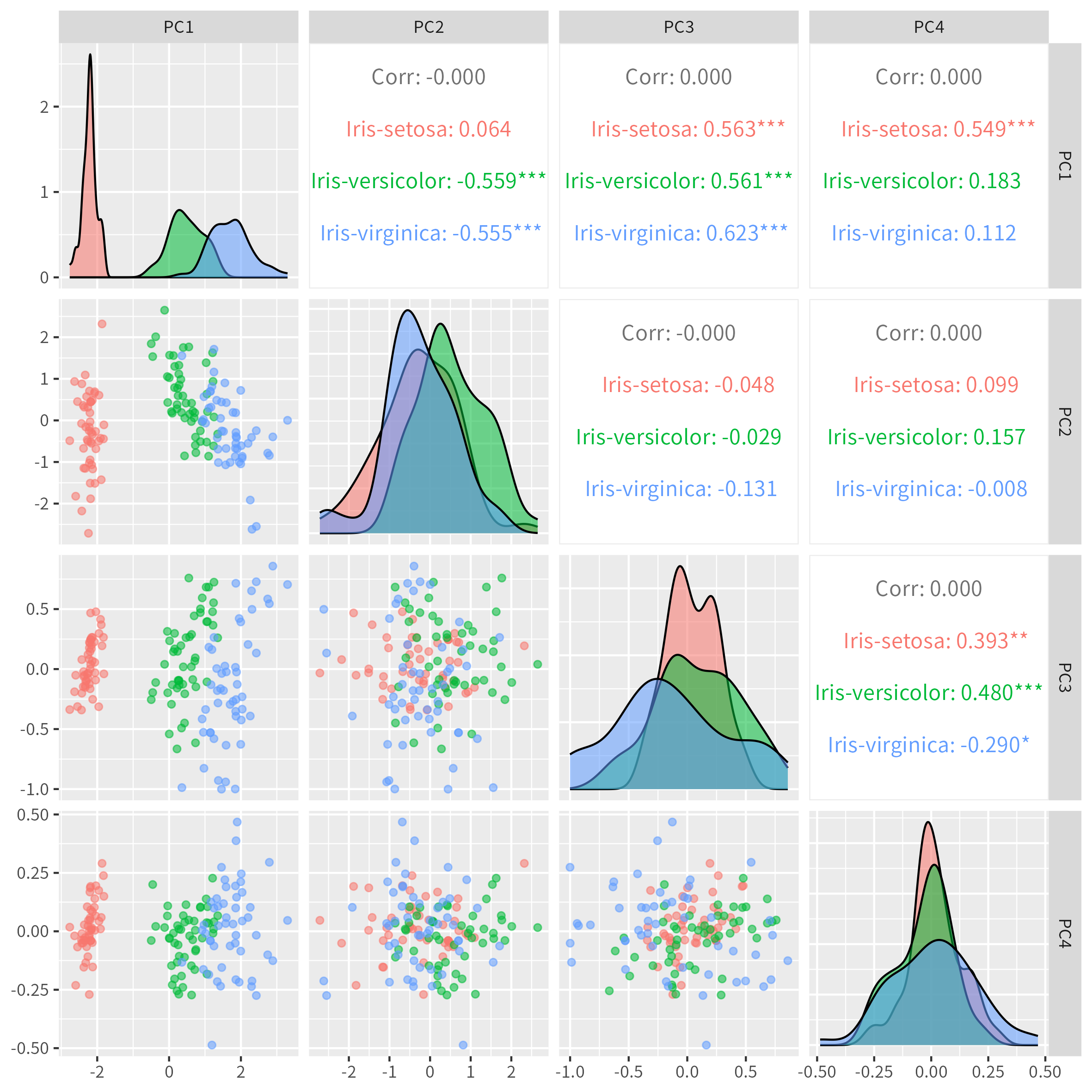
主成分を軸とした散布図を作成します。PC1 と PC2 だけで十分ですが、そもそも主成分は４つ（= 説明変数の数）までしかないので、全部の組み合わせをプロットしてしまいます。

p <- ggpairs(
    data = df.pca,
    columns = cols.pc,
    mapping = aes(color = Species, alpha = 0.5)
)
ggsave(
    filename = "iris_013_PCA_scatter.png", 
    plot = p, 
    width = 20, 
    height = 20, 
    units = "cm"
)
show(p)

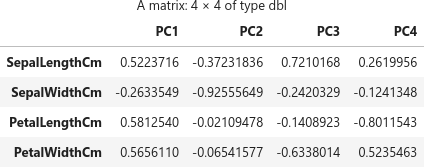
主成分に対する説明変数の寄与を確認します（主成分負荷量）。行列 (matrix) pca$rotation に情報が入っています。

pca$rotation

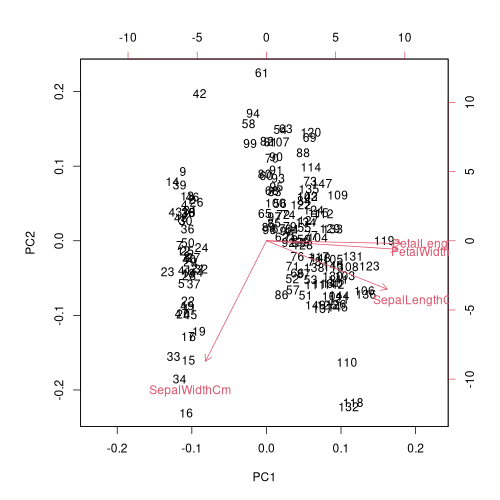
biplot 関数を使えば、主成分分析のスコアと主成分負荷量を一緒にプロットできます。

png("iris_014_loading.png", width = 500, height = 500)
biplot(pca, cex = 1)
dev.off()

Python / Scikit-Learn で主成分分析を扱った本ブログの記事 [1] の結果と比べると PC1 以外は符号が逆になっていますが、主成分分析の計算を考えると、主成分軸の正負の取り方で符号変わるのは仕方がないことなのでしょう。処理系によって符号の違いが出てくるかもしれないと認識しておく必要があります。

GUI やデータ解析でもなんでも Python でできてしまうので、重宝してよく使うようになりましたが、久しぶりに R を使って同じことをやってみると、R の方が便利だなと感じる点もあります、なにより、このように検証用に別の環境でできるようにしておくことが必要だと感じています。JupyterLab 上で Python も R も、おまけに Julia も使えるようになったので、今後もこうやって簡単なサンプルを使って、複数のプログラミング言語で比較を続けていく予定です。

トップへ