bitWalk's: 【備忘録】主成分分析～ Python / Scikit-Learn ～

主成分分析 (Principal Component Analysis, PCA) は、１観測あたり多数の次元／特徴を含む大規模データセットを分析し、最大限の情報量を保持しながらデータの解釈可能性を高め、多次元データの可視化を可能にする手法としてよく利用されています。形式的には、PCA はデータセットの次元を減少させる統計的手法です。これは、データの変動（の大部分）が、初期データよりも少ない次元で記述できるような新しい座標系にデータを線形変換することにより達成できます。

Wikipedia より引用、翻訳・編集

データ解析で頻繁に主成分分析 (PCA) を利用しています。主成分分析をはじめ、よく使用する機械学習の処理部分などは、いつも過去に使ったスクリプトから必要部分をコピペして使い回してしまっているので、思い違いや間違いがあれば、そのままずっと引きずってしまう可能性があります。ちょっと心配になってきたので、簡単なサンプルを使ってスクリプトを整理しようとしています。

今回は Python による主成分分析についてです。

下記の OS 環境で動作確認をしています。Fedora Linux 37 のデフォルトの Python のバージョンは 3.11.x ですが、新しすぎて一部のライブラリがまだ対応していない場合があるので、バージョン 3.10.y を使っています。

	Fedora Linux 37 Workstation	x86_64
	Python	3.10.9

今回は JupyterLab の Notebook 上で動作確認をしていますが、これをブログの記事に載せるにあたって、Gist を利用する方法よりは、スクリプトをブログ上にコピペする方が記事が作りやすいと考えたのですが、参考サイト [1] で紹介されている方法を使って、スクリプトの見映えを変えています。また、本記事作成用にデータフレームをイメージとして出力するために dataframe_image^[2]というモジュールを使用しています。

最初にプロット関連のモジュールを読み込んでおきます。また、フォントサイズは大きめに設定しています。

import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.size'] = 14

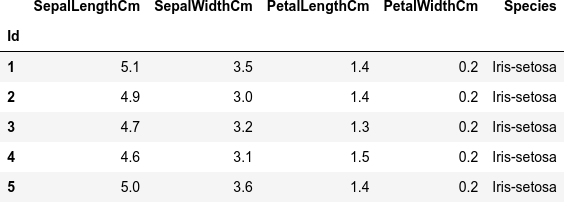
解析用のサンプルデータを読み込みます。解析用のサンプルは有名な Iris のデータセットを使っています。

Python のみで評価するのであれば、Scikit-Learn などで Iris のデータセットを利用できますが、Python 以外の言語でも確認したいと考えているので、同じデータソースを利用できるように、Kaggle のサイトで公開されている CSV データ Iris.csv [3] をダウンロードして使用しています。

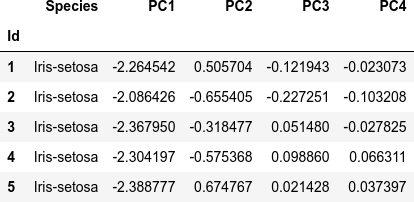
import pandas as pd
import dataframe_image as dfi

# https://www.kaggle.com/datasets/saurabh00007/iriscsv
filename = 'Iris.csv'
df = pd.read_csv(filename, index_col=0)
dfi.export(df.head(), 'table_001_iris.png')
df.head()

複数の変数（説明変数）x とターゲット（目的変数）y のカラムを定義しておきます。

cols_x = list(df.columns[0:4])
print('cols_x', cols_x)
col_y = df.columns[4]
print('col_y', col_y)

cols_x ['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm']
col_y Species

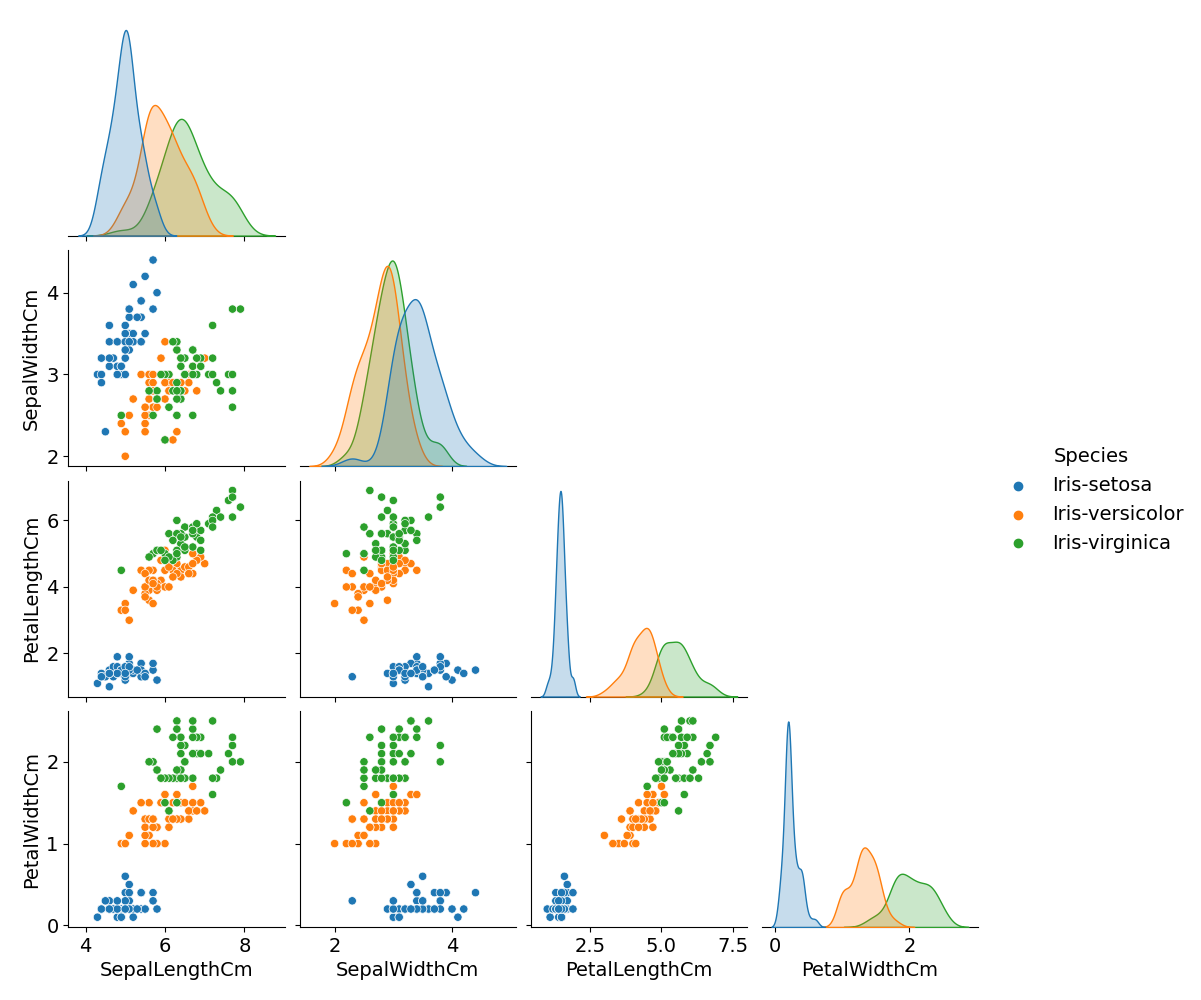
元データ（説明変数）の分布を散布図にして確認しておきます。

g = sns.pairplot(df, hue=col_y, corner=True)
g.fig.suptitle('Iris scatters', y=1.02)

plt.savefig('iris_001_scatter.png')
plt.show()

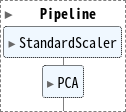
Scikit-Learn の StandardScaler と PCA をパイプラインでつなげて、モデルを定義します。

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

pipe = Pipeline(steps=[
    ('scaler', StandardScaler()),
    ('PCA', PCA()),
])

カラム x の説明変数のデータ（特徴量 features）でモデルの訓練をします。ここでは訓練データとテストデータには分けていません。ここではモデルの評価をしないので、説明変数のデータ全てを訓練データとして扱っています。

features = df[cols_x]
pipe.fit(features)

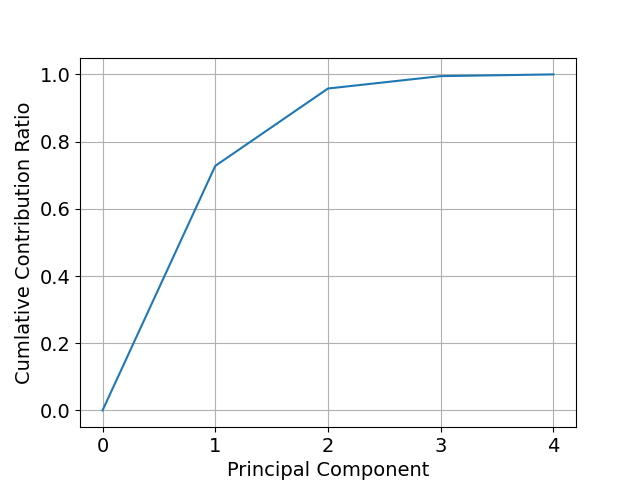
算出された主成分のばらつき（分散）に対する累積寄与率を計算してプロットします。

import numpy as np
import matplotlib.ticker as ticker

contribution_ratios = pipe['PCA'].explained_variance_ratio_
cumulative_contribution_ratios = np.hstack([0, contribution_ratios.cumsum()])

fig, ax = plt.subplots()
ax.plot(cumulative_contribution_ratios)
ax.set_xlabel('Principal Component')
ax.set_ylabel('Cumlative Contribution Ratio')

# this locator puts ticks at regular intervals
loc = ticker.MultipleLocator(base=1.0)
ax.xaxis.set_major_locator(loc)

plt.grid()
plt.savefig('iris_002_contrib.png')
plt.show()

最初の主成分 (PC1) と次の主成分 (PC2) だけで、データのばらつきの９割以上を説明できていることが判ります。

主成分得点をまとめたデータフレームを作成します。

scores = pipe.transform(features)
df_pca = pd.DataFrame(
    scores,
    columns=["PC{}".format(x + 1) for x in range(scores.shape[1])],
    index=df.index
)
df_pca.insert(0, col_y, df[col_y].copy())

dfi.export(df_pca.head(), 'table_002_iris_PCA.png')
df_pca.head()

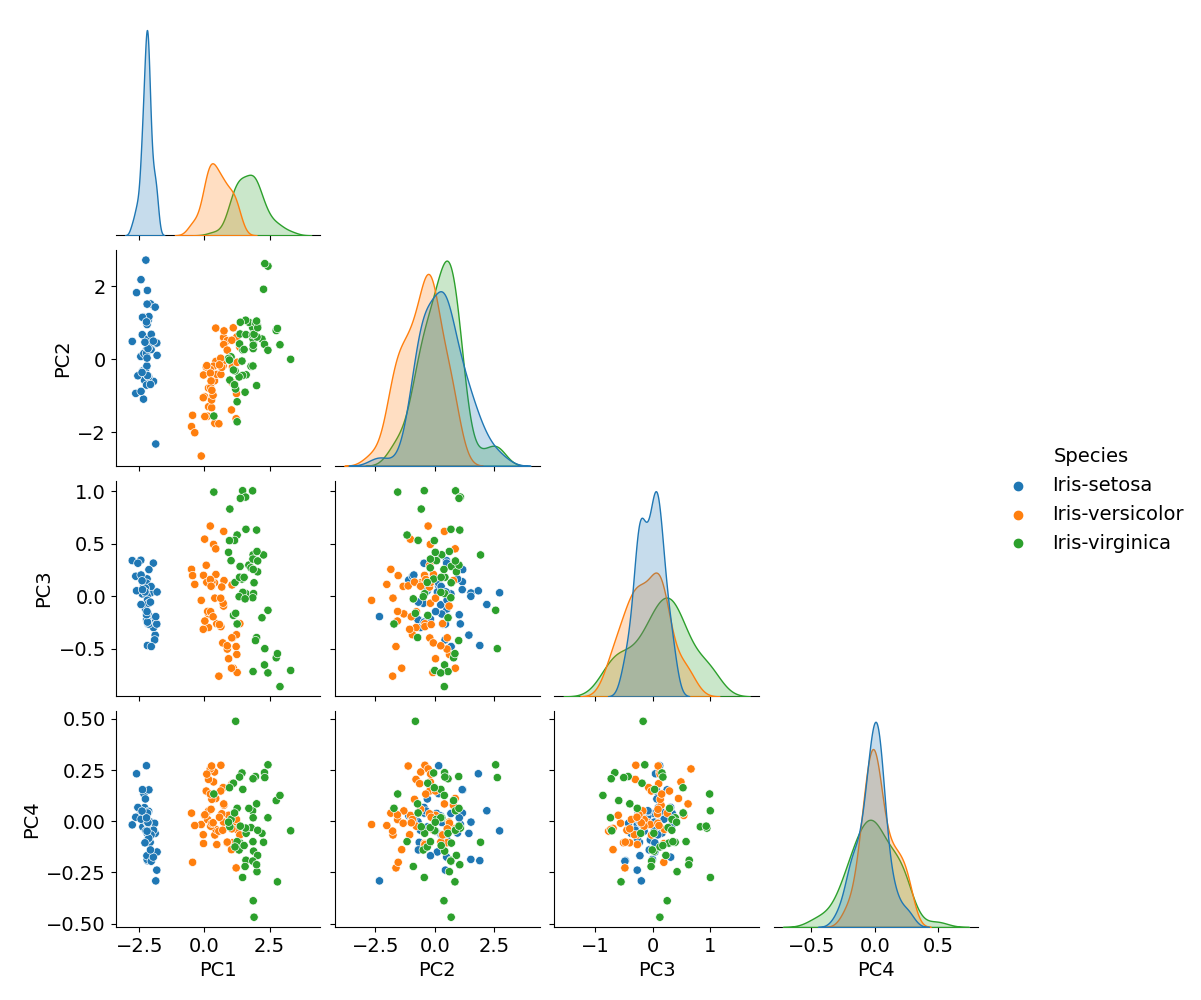
主成分を軸とした散布図を作成します。PC1 と PC2 だけで十分ですが、そもそも主成分は４つ（= 説明変数の数）までしかないので、全部の組み合わせをプロットしてしまいます。

g = sns.pairplot(df_pca, hue=col_y, corner=True)
g.fig.suptitle('Iris PCA score scatters', y=1.02)

plt.savefig('iris_003_PCA_scatter.png')
plt.show()

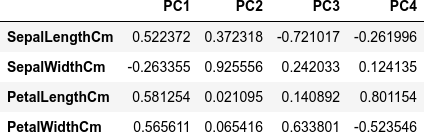
主成分に対する説明変数の寄与を確認します（主成分負荷量）。

components = pipe['PCA'].components_
df_load = pd.DataFrame(components.T,  index=features.columns, columns=["PC{}".format(x + 1) for x in range(len(components))])

dfi.export(df_load, 'table_003_iris_PCA_loading.png')
df_load

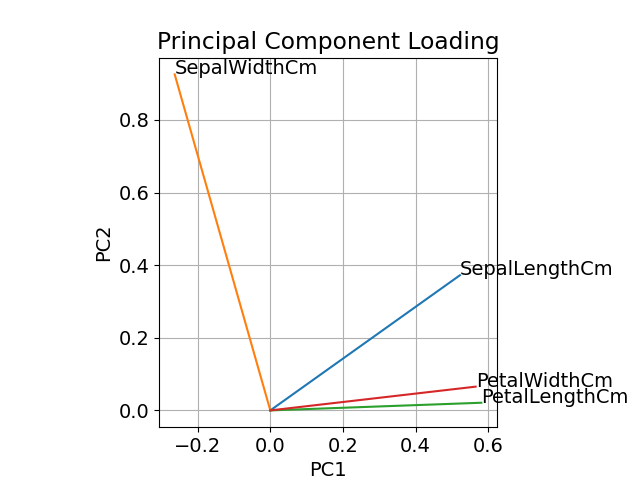
軸（PC1 と PC2）についてプロットしてみます。

pc_x = 'PC1'
pc_y = 'PC2'

fig, ax = plt.subplots()
for x, y, name in zip(df_load[pc_x], df_load[pc_y], df_load.index):
    ax.plot([0, x], [0, y])
    ax.text(x, y, name)

ax.set_xlabel(pc_x)
ax.set_ylabel(pc_y)
ax.set_title('Principal Component Loading')
ax.set_aspect('equal')

plt.grid()
plt.savefig('iris_004_loading.png')
plt.show()