bitWalk's: 【備忘録】主成分分析 (3) ～ Python / Scikit-Learn ～

主成分分析 (Principal Component Analysis, PCA) は、１観測あたり多数の次元／特徴を含む大規模データセットを分析し、最大限の情報量を保持しながらデータの解釈可能性を高め、多次元データの可視化を可能にする手法としてよく利用されています。形式的には、PCA はデータセットの次元を減少させる統計的手法です。これは、データの変動（の大部分）が、初期データよりも少ない次元で記述できるような新しい座標系にデータを線形変換することにより達成できます。

Wikipedia より引用、翻訳・編集

データ解析で頻繁に主成分分析 (PCA) を利用しています。主成分分析をはじめ、よく使用する機械学習の処理部分などは、いつも過去に使ったスクリプトから必要部分をコピペして使い回してしまっているので、思い違いや間違いがあれば、そのままずっと引きずってしまう可能性があります。ちょっと心配になってきたので、簡単なサンプルを使ってスクリプトを整理しようとしています。

もう少し、マハラノビス距離

前のブログ記事 [1] では、二次元に限定してマハラノビス距離を算出して、マハラノビス距離を等高線にして散布図に重ね合わせましたが、本記事ではもう少しマハラノビス距離を扱うことにします。

下記の OS 環境で動作確認をしています。

	Fedora Linux 37 Workstation	x86_64
	Python	3.10.9

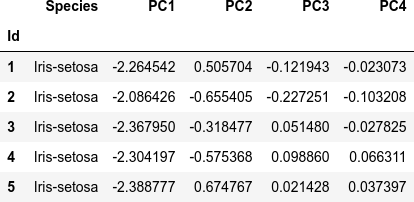
JupyterLab の Notebook 上で動作確認をしています。今回も、主成分分析の結果を利用してマハラノビス距離を算出しますので、まず、主成分分析をまとめて処理してしまいます。本ブログ記事 [2] で紹介した Iris データセットの主成分分析の処理を、必要な部分だけぎゅっとひとつにまとめました。

import pandas as pd
import dataframe_image as dfi
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
 
# https://www.kaggle.com/datasets/saurabh00007/iriscsv
filename = 'Iris.csv'
df = pd.read_csv(filename, index_col=0)
cols_x = list(df.columns[0:4])
col_y = df.columns[4]
 
# model pipeline for PCA
pipe = Pipeline(steps=[
    ('scaler', StandardScaler()),
    ('PCA', PCA()),
])
features = df[cols_x]
pipe.fit(features)
 
# PCA scores
scores = pipe.transform(features)
df_pca = pd.DataFrame(
    scores,
    columns=["PC{}".format(x + 1) for x in range(scores.shape[1])],
    index=df.index
)
cols_pc = list(df_pca.columns)
df_pca.insert(0, col_y, df[col_y].copy())
dfi.export(df_pca.head(), 'table_031_iris_PCA.png')
df_pca.head()

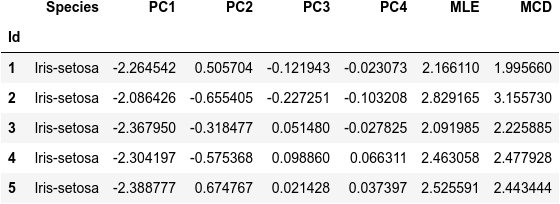
参考サイト [3] で紹介されている、MLE (The Maximum Likelihood Estimator) と MCD (The Minimum Covariance Determinant estimator) を用いた２つのマハラノビス距離を、二次元（２つの主成分）ではなく全ての主成分（と言っても、このサンプルでは PC1 ~ PC4 の４種類ですが…）を適用して算出します。

from sklearn.covariance import EmpiricalCovariance, MinCovDet
 
X = df_pca[cols_pc]
emp_cov = EmpiricalCovariance().fit(X)
robust_cov = MinCovDet().fit(X)
 
df_pca['MLE'] = emp_cov.mahalanobis(X)
df_pca['MCD'] = robust_cov.mahalanobis(X)
dfi.export(df_pca.head(), 'table_32_iris_PCA_MD.png')
df_pca.head()

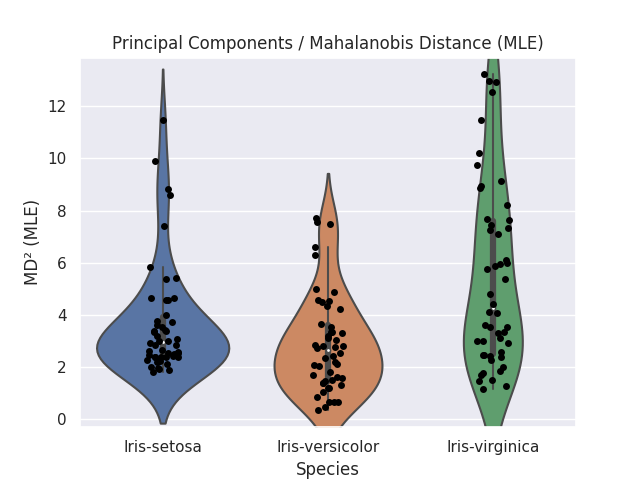
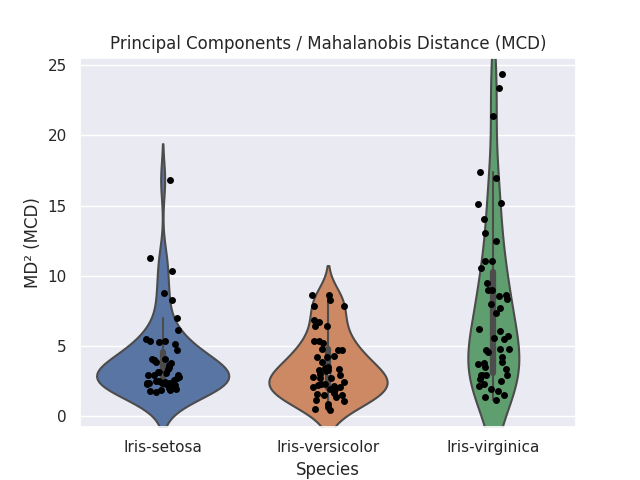
多次元を二次元の等高線でどう表現するかを考えると、どの断面を切り出すのが適当か判断できないので、さしあたって Violin Plot でプロットしてみました。

import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.size'] = 14
sns.set()
 
for md in ['MLE', 'MCD']:
    fig, ax = plt.subplots()
    sns.violinplot(data=df_pca, x='Species', y=md, showfliers=False, ax=ax)
    sns.stripplot(data=df_pca, x='Species', y=md, jitter=True, color='black', ax=ax)
 
    ax.set_ylabel('MD² (%s)' % md)
    ax.set_title('Principal Components / Mahalanobis Distance (%s)' % md)
    plt.savefig('iris_031_PCA_MD_%s.png' % md)
    plt.show()

二次元より大きい多次元データから算出したマハラノビス距離を、ユークリッド空間の二次元チャートに効果的に写像するのは難しいです。まずは、距離はそのまま距離として扱った方が良さそうです。時系列データといった順序のあるデータを扱う場合、マハラノビス距離は異常点の検出に威力を発揮することを期待しています。ブログで扱える適当な時系列的データセットがあれば、あらためてまとめたいと考えています。

トップへ