bitWalk's: 2023-01

2023-01-23

QThreadPool と QRunnable 〜 PySide6 〜

PySide (Qt for Python) は、Qt（キュート）の Python バインディングで、GUI などを構築するためのクロスプラットフォームなライブラリです。配布ライセンスは LGPL で公開されています。最新のバージョンは Qt6 に対応した PySide6（記事執筆時点で 6.4.2）です。

参考サイト [1] に QThreadPool と QRunnable を利用したマルチスレッディングの記事が判り易くまとめられていたので、早速記事を参考にしながら自分でもサンプルを作ってみました。

下記の OS 環境で動作確認をしました。

Fedora Linux 37	(Server Edition)	x86_64
python3.11	python3-3.11.1-3.fc37.x86_64
PySide6	6.4.2

qt_threadpool.py

	#!/usr/bin/env python
	# coding: utf-8

	import sys
	import time

	from PySide6.QtCore import (
	QObject,
	QRunnable,
	QThreadPool,
	Signal,
	Slot,
	)
	from PySide6.QtWidgets import (
	QApplication,
	QPlainTextEdit,
	QPushButton,
	QSizePolicy,
	QVBoxLayout,
	QWidget,
	)


	class WorkerSignal(QObject):
	progress = Signal(str)
	finished = Signal()


	class Worker(QRunnable):

	def __init__(self):
	super().__init__()
	self.signals = WorkerSignal()

	@Slot()
	def run(self):
	for count in range(0, 5):
	time.sleep(1)
	self.signals.progress.emit('%d%% done.' % (count * 100 / 4))
	self.signals.finished.emit()


	class Example(QWidget):
	log: QPlainTextEdit = None

	def __init__(self):
	super().__init__()
	self.threadpool = QThreadPool()
	self.init_ui()
	self.show_log(
	'Multithreading with maximum %d threads' % self.threadpool.maxThreadCount()
	)
	self.setWindowTitle('QThreadPool')
	self.resize(400, 200)

	def init_ui(self):
	layout = QVBoxLayout()
	self.setLayout(layout)

	btn = QPushButton('START')
	btn.setSizePolicy(QSizePolicy.Policy.Fixed, QSizePolicy.Policy.Fixed)
	btn.clicked.connect(self.button_clicked)
	layout.addWidget(btn)

	self.log = QPlainTextEdit()
	self.log.setMaximumBlockCount(1000)
	self.log.setSizePolicy(QSizePolicy.Policy.Expanding, QSizePolicy.Policy.Expanding)
	layout.addWidget(self.log)

	def button_clicked(self):
	obj = self.sender()
	self.show_log('%s button is clicked and starts thread task.' % obj.text())

	worker = Worker()
	worker.signals.progress.connect(self.show_log)
	worker.signals.finished.connect(self.thread_complete)
	self.threadpool.start(worker)

	def thread_complete(self):
	self.show_log('Thread completed!')

	def show_log(self, msg: str):
	self.log.insertPlainText(msg + '\n')


	def main():
	app = QApplication(sys.argv)
	ex = Example()
	ex.show()
	sys.exit(app.exec())


	if __name__ == '__main__':
	main()

view raw qt_threadpool.py hosted with ❤ by GitHub

別スレッド側では簡単な処理しかしていませんが、QThread でゴリゴリと記述するのに比べると、QThreadPool と QRunnable を利用すると、随分とスッキリ記述できました。

ただ、QRunnable と Signal を多重継承ができなかったので、Signal 用に別クラスを作らなければならなかったのが、ちょっと面倒なことぐらいです。

このサンプルでは START ボタンを続けてクリックすれば、スレッドが次々できますが、そのようなマルチスレッディングが必要な場面は、自分の用途ではとりあえずありません。むしろ、スレッドが処理している間は、同じ処理のスレッドができないように管理しなければならない場面のほうが多そうです。

トップへ

参考サイト

にほんブログ村

#オープンソース

2023-01-18

【備忘録】Python におけるループ変数のスコープ

なんかそうなんじゃないかな、と思っていたのですが、いままでしっかりと確認していませんでした。そもそも、必要がない限りはループ変数をループの外側では使わない癖みたいなものがあって、なんとなくループ外でループ変数を直接参照するのを避けていたような気がします。しかし、今回は気になって調べました。

いつもお世話になっている Stack Overflow に自分と同じ疑問を投稿したものがありました^[1]。少しだけ手直ししましたが下記の内容です。

for foo in range(10):
    bar = 2
print(foo, bar)

9 2

Python では、ループ変数はループ内だけで有効になっているわけではない（for 文はスコープを作らない）ということですが、C/C++ や Java ではありえない結果です。

念の為、正式な説明なるものを探したところ、参考サイト [2] を見つけました。

これはバグではなく、意図的に設計されたもので、Python 1 からずっとそうです。

ということです。

Python は、必要に迫られて使い始めたプログラミング言語ということもあって、そもそもまじめに一から学んでいません。自戒を込めて、プログラミング言語が違えば、スコープの扱い方も異なるということで備忘録にしました。

トップへ

参考サイト

scope - Scoping in Python 'for' loops - Stack Overflow [2010-08-31]
For Loop temporary variable scope should be local to For loop · Issue #88498 · python/cpython [2021-06-07]

にほんブログ村

#オープンソース

2023-01-13

QAbstractButton の利用〜 PySide6 〜

PySide6 で利用できる GUI のウィジェット（部品）は機能が豊富に備わっているので使っていて楽しいのですが、極めて大量かつ同じウィジェット（例えばチェックボックスだけのウィジェット）を表示したいときに、機能が豊富が故にインスタンスあたりのサイズが大きいのか、メモリがたくさん消費されて困ります。

そんな時、特定の目的に機能を絞った軽いウィジェットを作ることができれば、と考えました。チェックボックスのように抽象クラスの QAbstractButton^[1]を継承、実装しているボタン系ウィジェットであれば、必要な機能だけを実装したウィジェットを作れば、メモリの消費を抑えられるかもしれません。

そう考えて、まず QAbstractButton から作ったウィジェットのサンプルが公開されていないか探しました。なかなか都合の良い例がありませんでしたが、Toggle ウィジェット（クラス）^[2]というのを見つけましたので、PySide6 用に少し直して紹介します。なお、ここでは Swicth と、ウィジェット（クラス）の名前を変えました。

下記の OS 環境で動作確認をしました。

Fedora Linux 37	(Server Edition)	x86_64
python3.11	python3-3.11.1-1.fc37.x86_64
PySide6	6.4.2

抽象クラス QAbstractButton を直接継承して機能を実装した Switch クラスを下記に示しました。

qt_custom_switch.oy

	import sys

	from PySide6.QtCore import (
	QPropertyAnimation,
	QRect,
	QSize,
	Qt,
	Property,
	Signal,
	)
	from PySide6.QtGui import (
	QBrush,
	QColor,
	QPainter,
	)
	from PySide6.QtWidgets import (
	QAbstractButton,
	QApplication,
	QVBoxLayout,
	QWidget,
	)


	# Reference:
	# https://www.programcreek.com/python/?code=decred%2Ftinydecred%2Ftinydecred-master%2Ftinywallet%2Ftinywallet%2Fqutilities.py
	class Switch(QAbstractButton):
	"""Implementation of a clean looking toggle switch translated from
	https://stackoverflow.com/a/38102598/1124661
	QAbstractButton::setDisabled to disable
	"""
	statusChanged = Signal(bool)

	def __init__(self):
	super().__init__()
	self.onBrush = QBrush(QColor("#569167"))
	self.slotBrush = QBrush(QColor("#999999"))
	self.switchBrush = self.slotBrush
	self.disabledBrush = QBrush(QColor("#666666"))
	self.on = False
	self.fullHeight = 18
	self.halfHeight = self.xPos = int(self.fullHeight / 2)
	self.fullWidth = 34
	self.setFixedWidth(self.fullWidth)
	self.slotMargin = 3
	self.slotHeight = self.fullHeight - 2 * self.slotMargin
	self.travel = self.fullWidth - self.fullHeight
	self.slotRect = QRect(
	self.slotMargin,
	self.slotMargin,
	self.fullWidth - 2 * self.slotMargin,
	self.slotHeight,
	)
	self.animation = QPropertyAnimation(self, b'pqProp', self)
	self.animation.setDuration(120)
	self.setCursor(Qt.PointingHandCursor)

	def paintEvent(self, e):
	"""QAbstractButton method. Paint the button.
	"""
	painter = QPainter(self)
	painter.setPen(Qt.NoPen)
	painter.setBrush(self.switchBrush if self.on else self.disabledBrush)
	painter.setOpacity(0.6)
	painter.drawRoundedRect(
	self.slotRect, self.slotHeight / 2, self.slotHeight / 2,
	)
	painter.setOpacity(1.0)
	painter.drawEllipse(
	QRect(self.xPos, 0, self.fullHeight, self.fullHeight, )
	)

	def mouseReleaseEvent(self, e):
	"""Switch the button.
	"""
	if e.button() == Qt.LeftButton:
	self.on = not self.on
	self.switchBrush = self.onBrush if self.on else self.slotBrush
	self.animation.setStartValue(self.xPos)
	self.animation.setEndValue(self.travel if self.on else 0)
	self.animation.start()
	self.statusChanged.emit(self.on)
	super().mouseReleaseEvent(e)

	def sizeHint(self):
	"""Required to be implemented and return the size of the widget.
	"""
	return QSize(self.fullWidth, self.fullHeight)

	def setOffset(self, o):
	"""Setter for QPropertyAnimation.
	"""
	self.xPos = o
	self.update()

	def getOffset(self):
	"""Getter for QPropertyAnimation.
	"""
	return self.xPos

	pqProp = Property(int, fget=getOffset, fset=setOffset)

	def set(self, on):
	"""Set state to on, and trigger repaint.
	"""
	self.on = on
	self.switchBrush = self.onBrush if on else self.slotBrush
	self.xPos = self.travel if on else 0
	self.update()


	class Example(QWidget):
	"""Example widget for demonstration
	"""

	def __init__(self):
	super().__init__()
	self.setWindowTitle('Example for Switch')

	layout = QVBoxLayout()
	self.setLayout(layout)

	switch = Switch()
	switch.statusChanged.connect(self.switch_changed)
	layout.addWidget(switch)

	def switch_changed(self, status: bool):
	"""for statusChanged signal
	"""
	print('Switch is', status)


	def main():
	"""main event loop
	"""
	app: QApplication = QApplication(sys.argv)
	ex = Example()
	ex.show()
	sys.exit(app.exec())


	if __name__ == "__main__":
	main()

view raw qt_custom_switch.py hosted with ❤ by GitHub

Switch は小さなウィジェットです。実行例を示しました。

Switch is True

このサンプルで判ったことは、QAbstractButton を利用するには、ウィジェットを描画して表示する paintEvent メソッドと、表示サイズの推奨値を保持している sizeHint メソッドを、最低限オーバーライドして機能を実装する必要があるということでした。😁

さて、くだんのチェックボックスだけのウィジェットですが、QAbstractButtton を継承して、チェックボックスのチェック／アンチェックのイメージを切り替えて表示するようにしたものを作成したところ、これでメモリ使用量をざっくり３割程度に削減できました。これは 100 × 1000 以上の大きなチェックボックスのマトリックスを、スクロールバー付きで表示するような特殊な用途です。

トップへ

参考サイト

にほんブログ村

#オープンソース

2023-01-08

主成分分析 (Principal Component Analysis, PCA) は、１観測あたり多数の次元／特徴を含む大規模データセットを分析し、最大限の情報量を保持しながらデータの解釈可能性を高め、多次元データの可視化を可能にする手法としてよく利用されています。形式的には、PCA はデータセットの次元を減少させる統計的手法です。これは、データの変動（の大部分）が、初期データよりも少ない次元で記述できるような新しい座標系にデータを線形変換することにより達成できます。

Wikipedia より引用、翻訳・編集

データ解析で頻繁に主成分分析 (PCA) を利用しています。主成分分析をはじめ、よく使用する機械学習の処理部分などは、いつも過去に使ったスクリプトから必要部分をコピペして使い回してしまっているので、思い違いや間違いがあれば、そのままずっと引きずってしまう可能性があります。ちょっと心配になってきたので、簡単なサンプルを使ってスクリプトを整理しようとしています。

まずは主成分分析

今回の目的は、主成分分析で変換された主成分それぞれが、ターゲットに対してどの程度影響があるかを、一元配置分散分析（以降、単に分散分析と表します）を利用して検定することです。

下記の OS 環境で動作確認をしています。

	Fedora Linux 37 Workstation	x86_64
	Python	3.10.9

JupyterLab の Notebook 上で動作確認をしています。今回も主成分分析の結果を利用しますので、まず、主成分分析をまとめて処理してしまいます。本ブログ記事 [1] で紹介した Iris データセットの主成分分析の処理を、必要な部分だけぎゅっとひとつにまとめました。

import pandas as pd
import dataframe_image as dfi
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
 
# https://www.kaggle.com/datasets/saurabh00007/iriscsv
filename = 'Iris.csv'
df = pd.read_csv(filename, index_col=0)
dfi.export(df.head(), 'table_041_iris.png')
print(df.head())
cols_x = list(df.columns[0:4])
col_y = df.columns[4]
 
# model pipeline for PCA
pipe = Pipeline(steps=[
    ('scaler', StandardScaler()),
    ('PCA', PCA()),
])
features = df[cols_x]
pipe.fit(features)
 
# PCA scores
scores = pipe.transform(features)
df_pca = pd.DataFrame(
    scores,
    columns=["PC{}".format(x + 1) for x in range(scores.shape[1])],
    index=df.index
)
cols_pc = list(df_pca.columns)
df_pca.insert(0, col_y, df[col_y].copy())
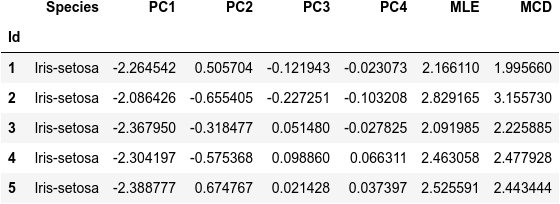
dfi.export(df_pca.head(), 'table_041_iris_PCA.png')
print(df_pca.head())

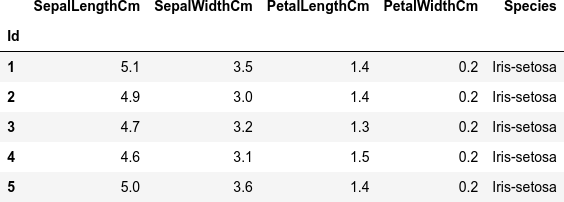
これが、読み込んだ Iris のデータセット df（最初の５行）です。

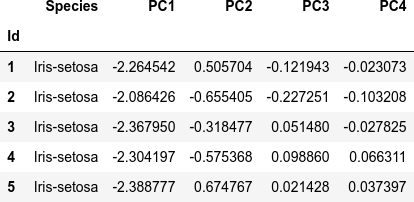
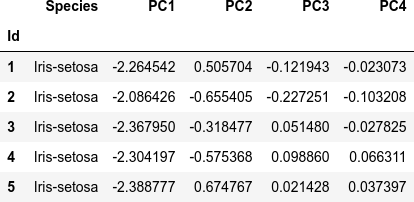
次が主成分分析をしたデータセット df_pca（最初の５行）です。

生データの分散分析

分散分析は SciPy の stats ライブラリの f_oneway を利用します。個々の因子 (SepalLengthCm, SepalWidthCm, PetalLengthCm, PetalWidthCm) に対し、ターゲット (Species) それぞれ (Iris-setosa, Iris-versicolor, Iris-virginica) の群をリストにまとめて、f_oneway() に渡します。

import numpy as np
from scipy import stats
 
list_species = list(set(df_pca[col_y]))
cols_stat = ['F-value', 'p-value']
 
df_anova = pd.DataFrame(columns=cols_stat)
for x in cols_x:
    args = [df[df[col_y] == list_species[i]][x] for i, species in enumerate(list_species)]
    f_value, p_value = stats.f_oneway(*args)
    result = pd.DataFrame(
        np.array([f_value, p_value]).reshape(1, 2),
        columns=cols_stat,
        index=[x]
    )
    # append row
    df_anova = pd.concat([df_anova, result], axis=0)
 
print(df_anova)

                   F-value       p-value
SepalLengthCm   119.264502  1.669669e-31
SepalWidthCm     47.364461  1.327917e-16
PetalLengthCm  1179.034328  3.051976e-91
PetalWidthCm    959.324406  4.376957e-85

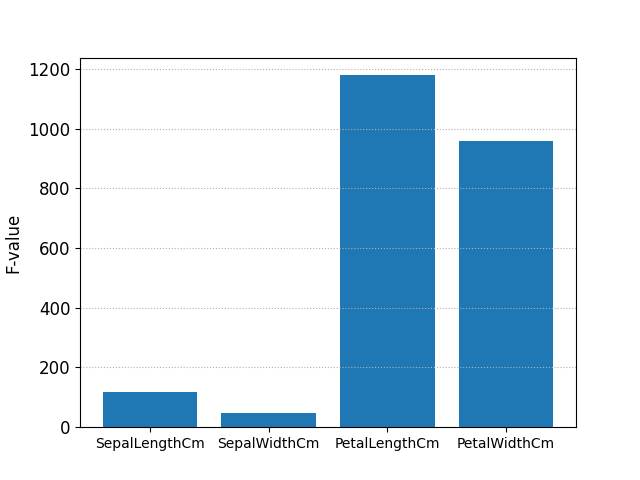
F-value を棒グラフにして表示します。

import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 12
 
fig, ax = plt.subplots()
plt.bar(df_anova.index, df_anova['F-value'])
ax.tick_params(axis='x', which='major', labelsize=10)
ax.set_ylabel('F-value')
plt.grid(axis='y',linestyle='dotted')
plt.savefig('iris_041_Oneway_ANOVA_raw.png')
plt.show()

主成分の分散分析

生データと同様に、主成分 (PC1 - PC4) に対しても分散分析をします。

df_pca_anova = pd.DataFrame(columns=cols_stat)
for pc in cols_pc:
    args = [df_pca[df_pca[col_y] == list_species[i]][pc] for i, species in enumerate(list_species)]
    f_value, p_value = stats.f_oneway(*args)
    result = pd.DataFrame(
        np.array([f_value, p_value]).reshape(1, 2),
        columns=cols_stat,
        index=[pc]
    )
    # append row
    df_pca_anova = pd.concat([df_pca_anova, result], axis=0)
 
print(df_pca_anova)

         F-value       p-value
PC1  1043.159859  1.412319e-87
PC2    14.429384  1.897877e-06
PC3     5.290448  6.043825e-03
PC4     1.636495  1.981874e-01

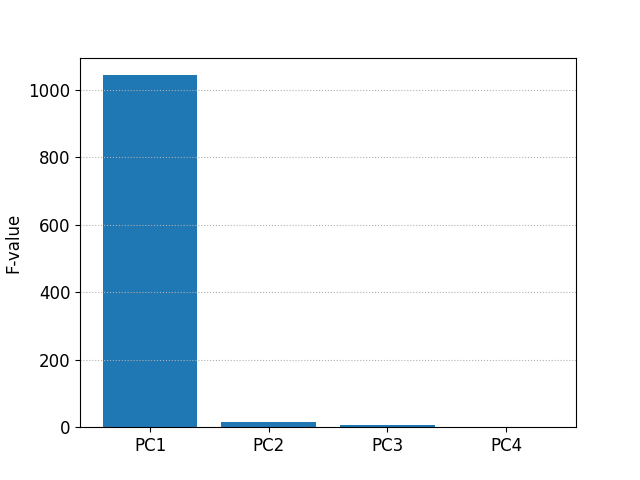
F-value を棒グラフにして表示します。

fig, ax = plt.subplots()
plt.bar(df_pca_anova.index, df_pca_anova['F-value'])
ax.set_ylabel('F-value')
plt.grid(axis='y',linestyle='dotted')
plt.savefig('iris_042_Oneway_ANOVA_PCA.png')
plt.show()

生データと主成分を分散分析した結果を比較して、あれこれ統計的な解釈をすることはできないのですが、主成分分析の結果、主成分１ (PC1) の影響がほとんどであるのに対し、生データでは PetalLengthCm（花弁の長さ）と PetalWidthCm（花弁の幅）の F-value が大きいことを考えると、Species の違いは花弁の長さと幅（= 面積？）で特徴づけられ、それは主成分分析をすると主成分１ (PC1) に現れていると考えられます。

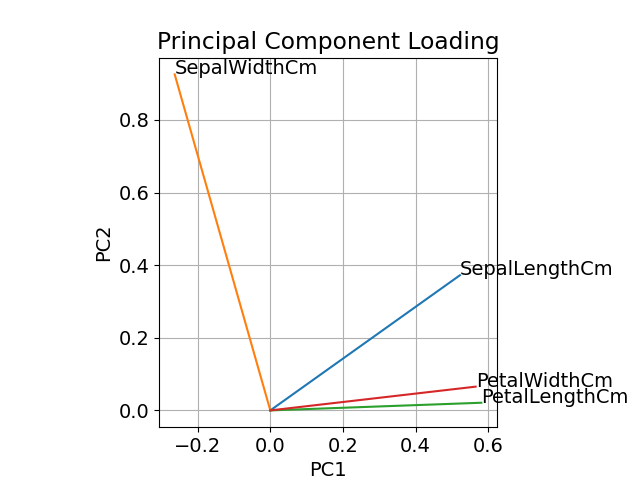
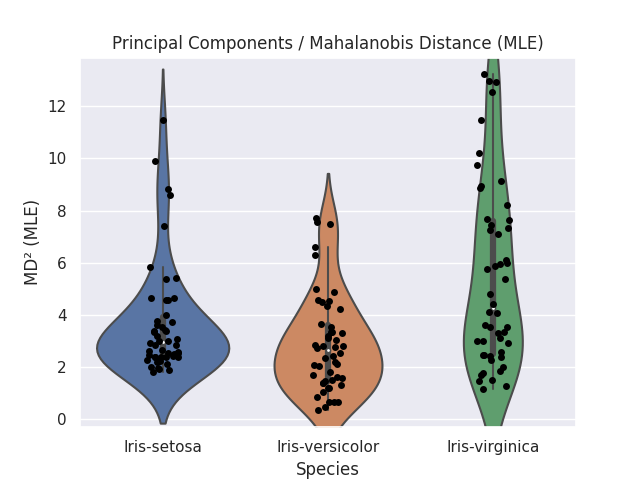
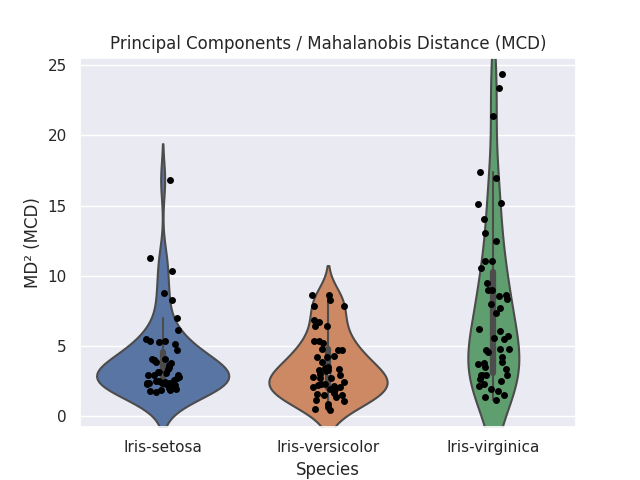
参考までに、本ブログ記事 [1] で紹介した主成分負荷量のプロットを再掲します。

scikit-learn による分散分析

結果は同じですが、scikit-learn の SelectKBest を利用しても分散分析ができます。主成分を分散分析すると次のようになります。

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
 
selector = SelectKBest(f_classif, k='all')
selector.fit(df_pca[cols_pc], df_pca[col_y])
print('features : ', selector.feature_names_in_)
print('scores   : ', selector.scores_)
print('p-values : ', selector.pvalues_)

features :  ['PC1' 'PC2' 'PC3' 'PC4']
scores   :  [1043.15985867   14.42938424    5.29044846    1.63649473]
p-values :  [1.41231945e-87 1.89787708e-06 6.04382459e-03 1.98187397e-01]

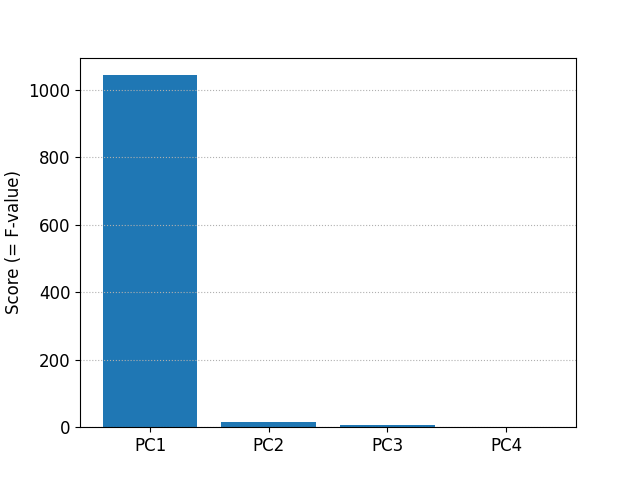
score (F-value) を棒グラフにして表示します。

fig, ax = plt.subplots()
plt.bar(selector.feature_names_in_, selector.scores_)
ax.set_ylabel('Score (= F-value)')
plt.grid(axis='y',linestyle='dotted')
plt.savefig('iris_043_Feature_Selection.png')
plt.show()

トップへ

参考サイト

bitWalk's: 【備忘録】主成分分析～ Python / Scikit-Learn ～ [2022-12-27]
bitWalk's: 【備忘録】主成分分析 (2) ～ Python / Scikit-Learn ～ [2023-01-03]
bitWalk's: 【備忘録】主成分分析 (3) ～ Python / Scikit-Learn ～ [2023-01-04]

にほんブログ村

#オープンソース

2023-01-04

【備忘録】主成分分析 (3) ～ Python / Scikit-Learn ～

Wikipedia より引用、翻訳・編集

もう少し、マハラノビス距離

前のブログ記事 [1] では、二次元に限定してマハラノビス距離を算出して、マハラノビス距離を等高線にして散布図に重ね合わせましたが、本記事ではもう少しマハラノビス距離を扱うことにします。

下記の OS 環境で動作確認をしています。

	Fedora Linux 37 Workstation	x86_64
	Python	3.10.9

JupyterLab の Notebook 上で動作確認をしています。今回も、主成分分析の結果を利用してマハラノビス距離を算出しますので、まず、主成分分析をまとめて処理してしまいます。本ブログ記事 [2] で紹介した Iris データセットの主成分分析の処理を、必要な部分だけぎゅっとひとつにまとめました。

import pandas as pd
import dataframe_image as dfi
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
 
# https://www.kaggle.com/datasets/saurabh00007/iriscsv
filename = 'Iris.csv'
df = pd.read_csv(filename, index_col=0)
cols_x = list(df.columns[0:4])
col_y = df.columns[4]
 
# model pipeline for PCA
pipe = Pipeline(steps=[
    ('scaler', StandardScaler()),
    ('PCA', PCA()),
])
features = df[cols_x]
pipe.fit(features)
 
# PCA scores
scores = pipe.transform(features)
df_pca = pd.DataFrame(
    scores,
    columns=["PC{}".format(x + 1) for x in range(scores.shape[1])],
    index=df.index
)
cols_pc = list(df_pca.columns)
df_pca.insert(0, col_y, df[col_y].copy())
dfi.export(df_pca.head(), 'table_031_iris_PCA.png')
df_pca.head()

参考サイト [3] で紹介されている、MLE (The Maximum Likelihood Estimator) と MCD (The Minimum Covariance Determinant estimator) を用いた２つのマハラノビス距離を、二次元（２つの主成分）ではなく全ての主成分（と言っても、このサンプルでは PC1 ~ PC4 の４種類ですが…）を適用して算出します。

from sklearn.covariance import EmpiricalCovariance, MinCovDet
 
X = df_pca[cols_pc]
emp_cov = EmpiricalCovariance().fit(X)
robust_cov = MinCovDet().fit(X)
 
df_pca['MLE'] = emp_cov.mahalanobis(X)
df_pca['MCD'] = robust_cov.mahalanobis(X)
dfi.export(df_pca.head(), 'table_32_iris_PCA_MD.png')
df_pca.head()

多次元を二次元の等高線でどう表現するかを考えると、どの断面を切り出すのが適当か判断できないので、さしあたって Violin Plot でプロットしてみました。

import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.size'] = 14
sns.set()
 
for md in ['MLE', 'MCD']:
    fig, ax = plt.subplots()
    sns.violinplot(data=df_pca, x='Species', y=md, showfliers=False, ax=ax)
    sns.stripplot(data=df_pca, x='Species', y=md, jitter=True, color='black', ax=ax)
 
    ax.set_ylabel('MD² (%s)' % md)
    ax.set_title('Principal Components / Mahalanobis Distance (%s)' % md)
    plt.savefig('iris_031_PCA_MD_%s.png' % md)
    plt.show()

二次元より大きい多次元データから算出したマハラノビス距離を、ユークリッド空間の二次元チャートに効果的に写像するのは難しいです。まずは、距離はそのまま距離として扱った方が良さそうです。時系列データといった順序のあるデータを扱う場合、マハラノビス距離は異常点の検出に威力を発揮することを期待しています。ブログで扱える適当な時系列的データセットがあれば、あらためてまとめたいと考えています。

トップへ

参考サイト

にほんブログ村

#オープンソース

登録: 投稿 (Atom)

bitWalk's

2023-01-23

QThreadPool と QRunnable 〜 PySide6 〜

参考サイト

2023-01-18

【備忘録】Python におけるループ変数のスコープ

参考サイト

2023-01-13

QAbstractButton の利用〜 PySide6 〜

参考サイト

2023-01-08

【備忘録】主成分分析と一元配置分散分析～ Python ～

まずは主成分分析

生データの分散分析

主成分の分散分析

scikit-learn による分散分析

参考サイト

2023-01-04

【備忘録】主成分分析 (3) ～ Python / Scikit-Learn ～

もう少し、マハラノビス距離

参考サイト

AddToAny

ブログアーカイブ

ノート

ラベル

Links

ページビューの合計

bitWalk's

2023-01-23

QThreadPool と QRunnable 〜 PySide6 〜

参考サイト

2023-01-18

【備忘録】Python におけるループ変数のスコープ

参考サイト

2023-01-13

QAbstractButton の利用 〜 PySide6 〜

参考サイト

2023-01-08

【備忘録】主成分分析と一元配置分散分析 ～ Python ～

まずは主成分分析

生データの分散分析

主成分の分散分析

scikit-learn による分散分析

参考サイト

2023-01-04

【備忘録】主成分分析 (3) ～ Python / Scikit-Learn ～

もう少し、マハラノビス距離

参考サイト

AddToAny

ブログ アーカイブ

ノート

ラベル

Links

ページビューの合計

QAbstractButton の利用〜 PySide6 〜

【備忘録】主成分分析と一元配置分散分析～ Python ～

ブログアーカイブ