bitWalk's: 【備忘録】Wilder の RSI

2024-09-05

【備忘録】Wilder の RSI

RSI, Relative Strength Index は、相場の過熱感を 0% - 100% で表したオシレーター系のテクニカル指標です。J・ウエルズ・ワイルダー・ジュニア氏 (J. Welles Wilder, Jr.) が考案者で、1978年に発表されました。日本語では、「相対力指数」と呼ばれます。

RSI の数値が 70% 以上では「買われすぎ」を意味し、30% 以下では「売られすぎ」を意味します。

算出方法は

RSI = 値上がり幅の指数移動平均(α) ÷ (値上がり幅の指数移動平均(α) ＋値下がり幅の指数移動平均(α)) × 100

α = 1/14 を使うことをワイルダーは推奨しています。つまり、14 日の修正移動平均です。

Wikipedia より引用・編集

先月 8 月 5 日の東京市場の歴史的な暴落を経験して、今さらながら先達が開発したテクニカル分析の手法を、自分でもプログラムを作って分析できるようにしようと思い、いろいろ調べています。

今回は上記 RSI です。

下記の OS 環境で動作確認をしています。

	RHEL 9.4	x86_64
	Python	3.12.1
	jupyterlab	4.2.5
	matplotlib	3.9.2
	mplfinance	0.12.10b0
	pandas	2.2.2
	yfinance	0.2.43

以下の作業は JupyterLab 上でおこなっています。

まず、必要なパッケージをインポートします。

import matplotlib.pyplot as plt
import mplfinance as mpf
import pandas as pd
import yfinance as yf

Wilder の RSI を算出する関数です。参考サイト [1] で公開されている Python のコードを流用させていただきました。

def wilder_rsi(ohlc: pd.DataFrame, period: int = 14) -> pd.Series:
    delta = ohlc['Close'].diff()

    up, down = delta.copy(), delta.copy()
    up[up < 0] = 0
    down[down > 0] = 0

    _gain = up.ewm(com=(period - 1), min_periods=period).mean()
    _loss = down.abs().ewm(com=(period - 1), min_periods=period).mean()

    rs = _gain / _loss
    return pd.Series(100 - (100 / (1 + rs)), name='RSI')

過去１年分の日経平均株価 (^N225) の日足データを取得します。

symbol = '^N225'
ticker = yf.Ticker(symbol)
df = ticker.history(period='1y')

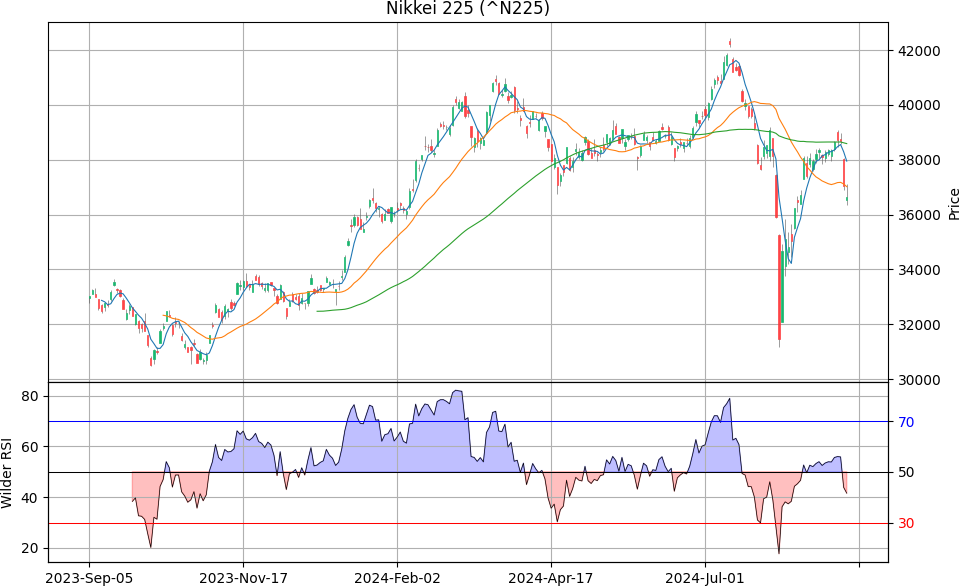
mplfinance でローソク足チャートとその移動平均（5 日, 25 日, 75 日）をプロットし、その下の二番目の領域に RSI をプロットします。チャートに手を加えたかったので mplfinance にプロットの全てを任せず、わざわざ matplotlib で扱えるようにしています。

# Wilder RSI
rsi = wilder_rsi(df)

fig, ax = plt.subplots(
    2, 1,
    gridspec_kw=dict(height_ratios=[2, 1], hspace=0),
    sharex=True, figsize=(12, 6)
)

apd_osc = [
    mpf.make_addplot(rsi, ylabel='RSI', color='black', width=0.5, ax=ax[1])
]

mpf.plot(
    df,
    type='candle',
    style='yahoo',
    mav=(5, 25, 75),
    addplot=apd_osc,
    ax=ax[0],
)

ax[0].set_title('%s (%s)' % (ticker.info['longName'], symbol))
ax[0].grid('both')

fb_rsi_up = dict(x=range(len(rsi)), y1=rsi.values, y2=50, where=50<rsi, color='blue', alpha=0.25, interpolate=True)
fb_rsi_dn = dict(x=range(len(rsi)), y1=rsi.values, y2=50, where=50>rsi, color='red', alpha=0.25, interpolate=True)
ax[1].fill_between(**fb_rsi_up)
ax[1].fill_between(**fb_rsi_dn)

ax[1].set_ylabel('Wilder RSI')
ax[1].grid('both')

ax2 = ax[1].twinx()
ax2.set_ylim(ax[1].get_ylim())
ax2.tick_params(axis='y')
ax2.set_yticks([30, 50, 70])
yticklabels2 = ax2.get_yticklabels()
yticklabels2[0].set_color('red')
yticklabels2[1].set_color('black')
yticklabels2[2].set_color('blue')
ax2.axhline(y=30, color='red', linewidth=0.75, linestyle='solid')
ax2.axhline(y=50, color='black', linewidth=0.75, linestyle='solid')
ax2.axhline(y=70, color='blue', linewidth=0.75, linestyle='solid')

plt.subplots_adjust(left=0.15, right=0.85, bottom=0.05, top=0.95)
# plt.savefig('rsi_wilder_n225.png')
plt.show()