bitWalk's: 【備忘録】フィボナッチ・リトレースメント

フィボナッチ数列を知ったのは数列や漸化式を習ったときですから、高校数学（数学ⅡB）の時だったしょうか。フィボナッチ数列の漸化式は簡単におぼえられましたし、不思議な性質があることも、解説を読んで知った気にはなっていました。しかし、実際の分析でフィボナッチ数列を活用することはありませんでした。

株式の取引をするようになって、ラジオ日経の「マーケットプレス」を聞いていると、ときどきフィボナッチ・リトレースメントを用いた分析例が紹介されます。先週の歴史的な東京市場の暴落を経験して、長期的な視点で、フィボナッチ・リトレースメントなるもので自分でも分析できるようにしようと思い、やり方をまとめました。

注意：下記の数式は、スマホのブラウザでは正しく表示されない場合があります。あらかじめご了承ください。

フィボナッチ数列

フィボナッチ数列は、次の漸化式で定義されます。

${\begin{cases}F_{0}=0&\,\\F_{1}=1&\,\\F_{n}=F_{n-1}+F_{n-2}&(n\geqq 2)\end{cases}}$

フィボナッチ数列の隣接2項の商は黄金比 φ に収束します。この性質は初期値 (F₀ = 0, F₁ = 1) に依存しません。

$\lim _{n\to \infty }{\frac {F_{n}}{F_{n-1}}}=\phi$

ただし

$\phi ={\frac {1+{\sqrt {5}}}{2}}=1.618033988749894\cdots$

なお、φ は以下の方程式の解の一つです。

$x^{2}-x-1=0$

Wikipedia より引用・編集

フィボナッチ・リトレースメント

フィボナッチ・リトレースメントとは、チャート上の下値支持線（サポートライン）や上値抵抗線（レジスタンスライン）を導出するテクニカル分析の一手法です。名前は、この手法がフィボナッチ数列を利用することに由来しています。フィボナッチ・リトレースメントは、市場が、予測可能な一定割合の反発あるいは反落の後、本来の方向への値動きを続ける、という考えに基づいています。

フィボナッチ・リトレースメントは、チャート上で２つの極値（上値と下値）を取り、その差分を主要なフィボナッチ比率で分割することで得られます。0.0% は反発/反落の始点とされ、100.0% が本来の値動きに対する完全な反発/反落です。ひとたびこれらの水準が決まれば、数本の水平線がサポートとレジスタンスの想定水準を示すものとして描かれます。

利用される主要なフィボナッチ比率は下記の３つです。前述の方程式の関係を利用してあれこれ変形すると、φ のべき乗の逆数になります。

［水準１］フィボナッチ数列上の数を、その直後の数で割ることで得られる値：

$\lim _{n\to \infty }{\frac {F_{n}}{F_{n+1}}}={\frac {1}{\phi}} \approx 0.618 = 61.8\%$

［水準２］フィボナッチ数列上の数を、その2つ後の数で割ることで得られる値：

$\lim _{n\to \infty }{\frac {F_{n}}{F_{n+2}}}={\frac {\phi - 1}{\phi}}={\frac {\phi^{2} - \phi}{\phi^{2}}}={\frac {1}{\phi^{2}}}\approx{0.382}={38.2}\%$

［水準３］フィボナッチ数列上の数を、その3つ後の数で割ることで得られる値：

$\lim _{n\to \infty }{\frac {F_{n}}{F_{n+3}}}={\frac {{2}-\phi}{\phi}}={\frac {{2}\phi^{2}-\phi^{3}}{\phi^{3}}}={\frac {\phi^{2}+\phi(\phi-\phi^{2})}{\phi^{3}}} ={\frac {\phi^{2}-\phi}{\phi^{3}}}={\frac {1}{\phi^{3}}}\approx 0.236 = 23.2\%$

Wikipedia より引用・編集

例えば、上昇トレンド中に一時的に下落した場合、直近の高値と安値を結んで引いたフィボナッチ・リトレースメントの上記 23.6%, 38.2%, 61.8% のラインを反発の可能性が高い水準として注視します。

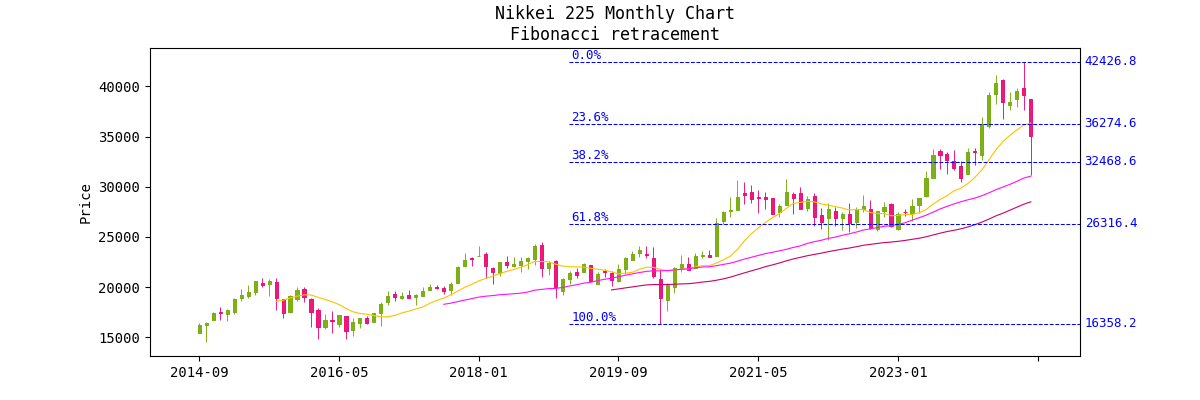
日経平均株価の最高値とその後の暴落

ラジオ日経のマーケットプレス８月９日後場の番組で紹介された分析^[1]と同じように、7 月に記録した日経平均株価の最高値と先週月曜日の歴史的な大暴落を、コロナショックの暴落を起点に分析してみます。

下記の OS 環境で動作確認をしています。

	RHEL 9.4	x86_64
	Python	3.12.1
	jupyterlab	4.2.4
	matplotlib	3.9.1.post1
	mplfinance	0.12.10b0
	pandas	2.2.2
	yfinance	0.2.41

以下の作業は JupyterLab 上でおこなっています。

まず、必要なパッケージをインポートします。

import matplotlib.pyplot as plt
import mplfinance as mpf
import pandas as pd
import yfinance as yf

日経平均株価の yf.Ticker インスタンスを生成します。

symbol = '^N225'
ticker = yf.Ticker(symbol)

過去１０年分の月足データを取得します。

df = ticker.history(period='10y', interval='1mo')
df

水準の決定

2020 年 3 月の日経平均株価

月次終値としては2017年３月（１万8909円26銭）以来、３年ぶりの水準に落ち込んだ。新型コロナウイルスの感染者が世界的に増え続け、終息の兆しが見えないなか、実体経済への影響を警戒した売りが広がった。原油安や急速な円高・ドル安を受け、運用リスクを回避する株売りも目立った。

2020年3月の日経平均株価:指数リポート [2] より

2020 年 3 月の安値を 100% の水準にします。決め打ちで抽出しても良いのですが、ここでは月足データから、2018 年 1 月以降の安値の最小値（= 2020 年 3 月の安値）を求める処理をしています。

origin = pd.to_datetime('2018-01-01 00:00:00+09:00')
price_min = min(df[df.index > origin]['Low'])
df_min = df[df['Low'] == price_min]
ts_min = df_min.index[0]
print(ts_min, price_min)

2020-03-01 00:00:00+09:00 16358.1904296875

2024 年 7 月の日経平均株価

７月前半は米連邦準備理事会（ＦＲＢ）の早期利下げへの期待を背景に、米国市場でハイテク株が上昇。東京市場でも半導体関連株が買われて日経平均が上昇し、11日には４万2224円02銭と終値で史上初めて４万2000円台を記録した。

2024年7月の日経平均株価:指数リポート [3] より

2024 年 7 月の高値を 0% の水準にします。単純に抽出したデータの高値から最大値を求めます。

price_max = max(df['High'])
df_max = df[df['High'] == price_max]
ts_max = df_max.index[0]
print(ts_max, price_max)

2024-07-01 00:00:00+09:00 42426.76953125

23.6%, 38.2%, 61.8% の水準の値を求めます。

delta = price_max - price_min
level1 = price_max - 0.236 * delta
level2 = price_max - 0.382 * delta
level3 = price_max - 0.618 * delta

以上の情報を利用して、mplfinance で描画したローソク足チャートにフィボナッチ・リトレースメントの水準を追加します。

plt.rcParams['font.family'] = 'monospace'
fig, ax = plt.subplots(figsize=(12, 4))
 
mpf.plot(
    df,
    type='candle',
    style='binance',
    datetime_format='%Y-%m',
    xrotation=0,
    mav=(12, 36, 60),
    ax = ax,
)
 
# フィボナッチリトレースメント
x_start = 0.45
x_left = ax.get_xlim()[0]
x_right = ax.get_xlim()[1]
x_mid = (x_right - x_left) * (x_start - 0.05)
x_delta = x_right - x_left
x_adjust = x_delta * 0.005
 
y_min = ax.get_ylim()[0]
y_max = ax.get_ylim()[1]
y_delta = y_max - y_min
y_adjust = y_delta * 0.01
 
for y, v in zip([price_max, level1, level2, level3, price_min],[0, 23.6, 38.2, 61.8, 100]):
    plt.axhline(y, xmin=x_start, linestyle = 'dashed', linewidth=0.75, color = 'b')
    plt.text(x_right + x_adjust, y - y_adjust, '%.1f' % y, color='b', fontsize=9)
    plt.text(x_mid, y + y_adjust, '%.1f%%' % v, color='b', fontsize=9)
 
plt.title('Nikkei 225 Monthly Chart\nFibonacci retracement')
plt.savefig('n255_fibonacci.png')
plt.show()