主成分分析 (Principal Component Analysis, PCA) は、1観測あたり多数の次元/特徴を含む大規模データセットを分析し、最大限の情報量を保持しながらデータの解釈可能性を高め、多次元データの可視化を可能にする手法としてよく利用されています。形式的には、PCA はデータセットの次元を減少させる統計的手法です。これは、データの変動(の大部分)が、初期データよりも少ない次元で記述できるような新しい座標系にデータを線形変換することにより達成できます。
データ解析で頻繁に主成分分析 (PCA) を利用しています。主成分分析をはじめ、よく使用する機械学習の処理部分などは、いつも過去に使ったスクリプトから必要部分をコピペして使い回してしまっているので、思い違いや間違いがあれば、そのままずっと引きずってしまう可能性があります。ちょっと心配になってきたので、簡単なサンプルを使ってスクリプトを整理しようとしています。
今回は Python による主成分分析において、2つのクラスタを特定して、その差に寄与する因子(特徴量)の重要度 (Feature Importance) を評価します。
下記の OS 環境で動作確認をしています。Fedora Linux 38 のデフォルトの Python のバージョンは 3.11.x ですが、一部のライブラリがまだ対応していないので一つ前のバージョン 3.10.y を使っています。

|
Fedora Linux 38 | x86_64 |
| Python | 3.10.11 |
JupyterLab の Notebook 上で動作確認をしています。まず、主成分分析をまとめて処理してしまいます。本ブログ過去記事 [1] で紹介した Iris データセットの主成分分析の処理を、必要な部分だけぎゅっとひとつにまとめました。
import pandas as pd
import dataframe_image as dfi
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# https://www.kaggle.com/datasets/saurabh00007/iriscsv
filename = 'Iris.csv'
df = pd.read_csv(filename, index_col=0)
cols_x = list(df.columns[0:4])
col_y = df.columns[4]
name_target = sorted(list(set(df[col_y])))
# model pipeline for PCA
pipe = Pipeline(steps=[
('scaler', StandardScaler()),
('PCA', PCA()),
])
features = df[cols_x]
pipe.fit(features)
# PCA scores
scores = pipe.transform(features)
df_pca = pd.DataFrame(
scores,
columns=["PC{}".format(x + 1) for x in range(scores.shape[1])],
index=df.index
)
cols_pc = list(df_pca.columns)
df_pca.insert(0, col_y, df[col_y].copy())
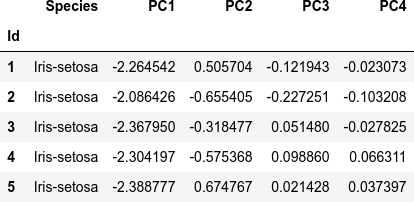
dfi.export(df_pca.head(), 'table_061_iris_PCA.png')
df_pca.head()
主成分を軸とした散布図を作成します。主成分は4つ(= 説明変数の数)しかないので、全部の組み合わせをプロットします。
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.size'] = 14
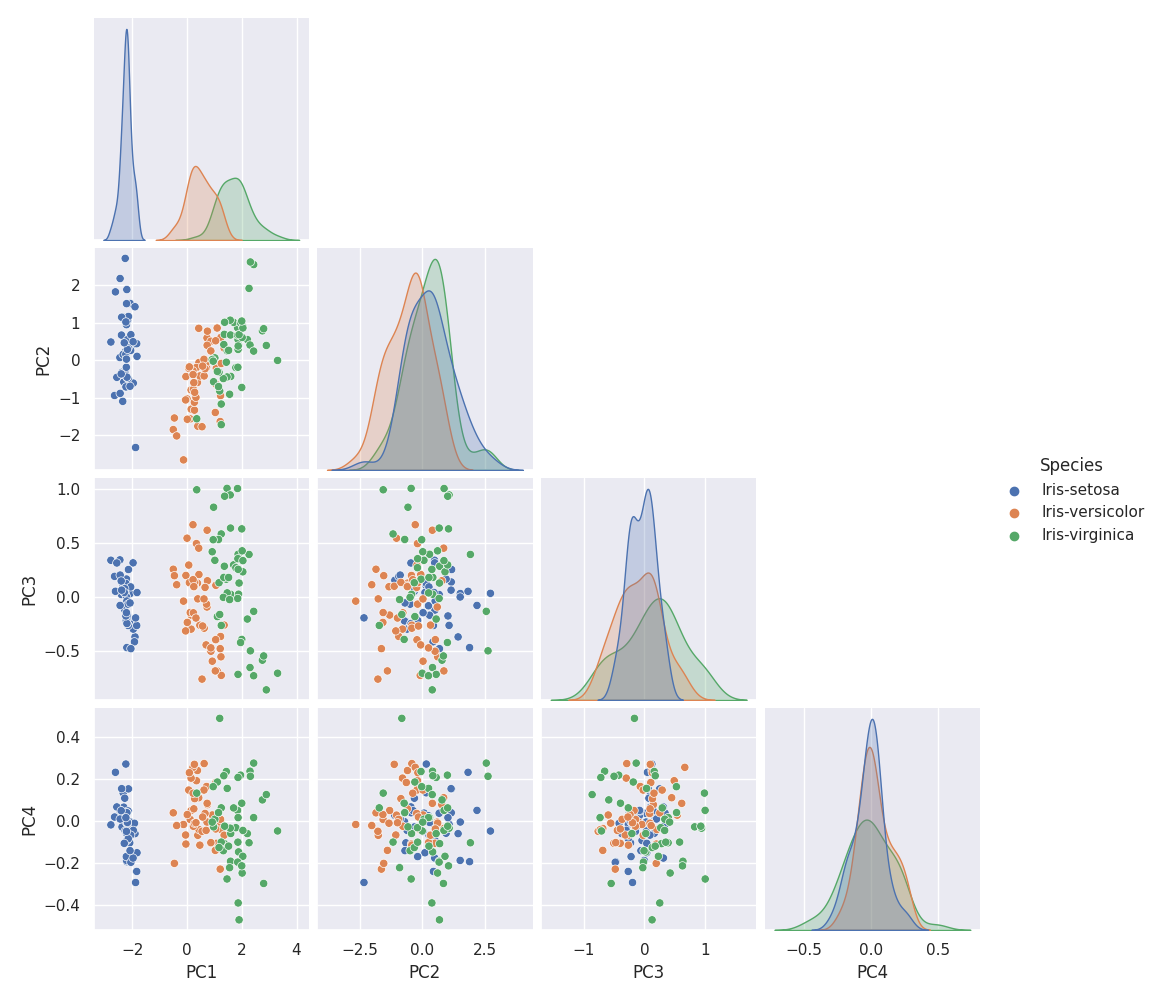
g = sns.pairplot(df_pca, hue=col_y, corner=True)
g.fig.suptitle('Iris PCA score scatters', y=1.02)
plt.savefig('iris_061_PCA_scatter.png')
plt.show()
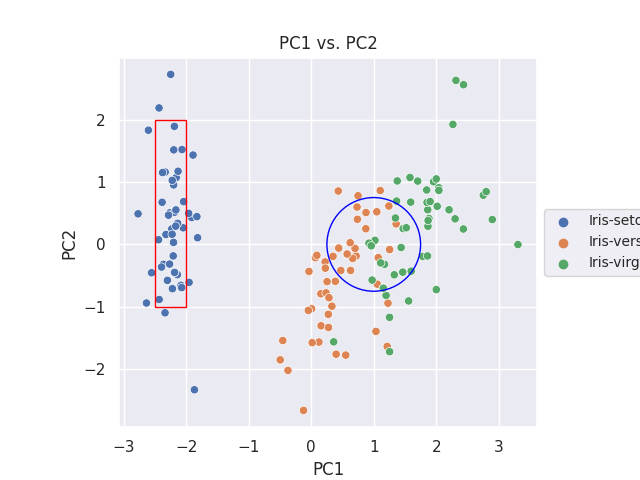
2つのクラスタの特定
分布の差を調べたい2つのクラスタを特定します。ここでは主成分 PC1 と PC2 に注目し、下記のように赤枠と青丸で囲んだ内側のデータ群を調べることにします。
import matplotlib.patches as patches
fig, ax = plt.subplots()
sns.scatterplot(data=df_pca, x='PC1', y='PC2', hue=col_y, ax=ax)
ax.set_aspect('equal')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5), fontsize=10)
ax.set_title('PC1 vs. PC2')
x1 = -2.5
y1 = -1.0
w1 = 0.5
h1 = 3.0
c1 = patches.Rectangle(xy=(x1, y1) , width=w1, height=h1, fill=False, edgecolor='red')
ax.add_patch(c1)
x2 = 1.0
y2 = 0.0
r2 = 0.75
c2 = patches.Circle(xy=(x2, y2), radius=r2, fill=False, edgecolor='blue')
ax.add_patch(c2)
plt.savefig('iris_062_PCA_PC1PC2.png')
plt.show()
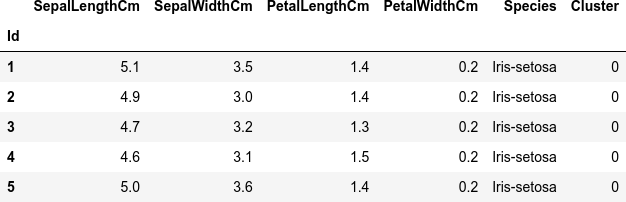
赤枠 (Cluster 0) と青丸 (Cluster 1) で囲んだデータ点に対応する元のデータを、Cluster 列にそれぞれ 0、1 と付けて抽出して連結します。
col_cluster = 'Cluster' # Cluster 0 df_cluster_0 = df[(df_pca['PC1'] > x1) & (df_pca['PC1'] < (x1 + w1)) & (df_pca['PC2'] > y1) & (df_pca['PC2'] < (y1 + h1))].copy() df_cluster_0[col_cluster] = 0 # Cluster 1 df_cluster_1 = df[((df_pca['PC1'] - x2)**2 < r2**2) & ((df_pca['PC2'] - y2)**2 < r2**2)].copy() df_cluster_1[col_cluster] = 1 # concatenate 2 clusters df_cluster = pd.concat([df_cluster_0, df_cluster_1]) dfi.export(df_cluster.head(), 'table_062_iris_PCA_cluster.png') df_cluster
Random Forest による分類
特定した2つのクラスタを、ここでは Random Forest の分類器を使って分類します。
from sklearn.ensemble import RandomForestClassifier
from sklearn.preprocessing import StandardScaler
X = df_cluster[cols_x]
y = df_cluster[col_cluster]
pipe = Pipeline([
('scaler', StandardScaler()),
('RF', RandomForestClassifier(random_state=42))
])
pipe.fit(X, y)
特徴量の重要度の評価
fit した分類結果より、2つのクラスタの差(= 分類)に寄与する因子(特徴量)の重要度 (Feature Importance) を評価します。いくつか算出方法がありますので、主要なやりかたをいくつか利用してみます。
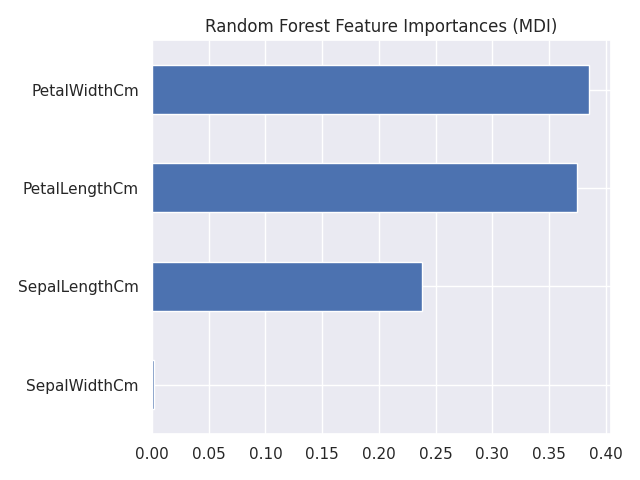
Mean Decrease in Impurity (MDI)
まずは、RandomForest 分類器の feature_importances_ をそのまま利用した場合の計算です。これは、平均不純度変少量(Mean Decrease Impurity; MDI)あるいはジニ重要度(gini importance)と呼ばれる重要度です [3]。
feature_names = X.columns
mdi_importances = pd.Series(
pipe['RF'].feature_importances_, index=feature_names
).sort_values(ascending=True)
ax = mdi_importances.plot.barh()
ax.set_title("Random Forest Feature Importances (MDI)")
ax.figure.tight_layout()
plt.savefig('iris_071_feature_inportance_mdi.png')
plt.show()
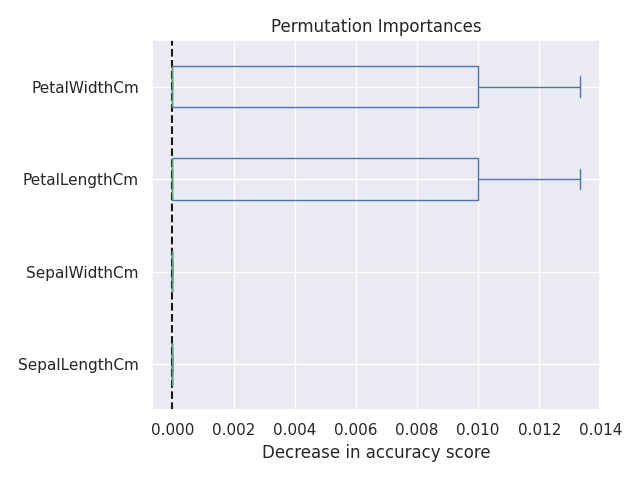
Permutation Importance
Permutation Importance は、元のデータから算出した予測精度と、特徴量の値を並び替えて (permutation) 算出した予測精度を比較して、精度の減少が大きいものをより重要な特徴量と判断しています [4]。
from sklearn.inspection import permutation_importance
result = permutation_importance(pipe, X, y, n_repeats=10, random_state=42, n_jobs=2)
sorted_importances_idx = result.importances_mean.argsort()
importances = pd.DataFrame(
result.importances[sorted_importances_idx].T,
columns=X.columns[sorted_importances_idx],
)
ax = importances.plot.box(vert=False, whis=10)
ax.set_title('Permutation Importances')
ax.axvline(x=0, color='k', linestyle='--')
ax.set_xlabel('Decrease in accuracy score')
ax.figure.tight_layout()
plt.savefig('iris_072_feature_inportance_purmutation.png')
plt.show()
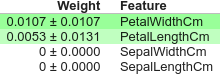
Permutation Importance の算出には、eli5 というパッケージを利用することもできます。
import eli5 from eli5.sklearn import PermutationImportance perm = PermutationImportance(pipe) perm.fit(X, y) eli5.show_weights(perm, feature_names=X.columns.tolist())
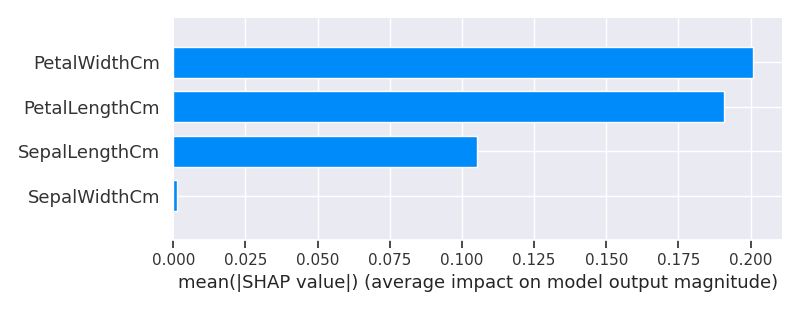
SHAP を用いた特徴量のインパクト
SHAP(SHapley Additive exPlanations)は、協力ゲーム理論のシャープレイ値(Shapley Value)を近似的に算出して機械学習に応用できるようにしたパッケージです。
SHAP では特徴量のインパクトを算出できます、これは各特徴量の貢献度の平均値の絶対値を表示したものです。これによりどの特徴量がモデルに効いているかを確認することができます。これを特徴量の重要度として扱います [5]。
import shap
shap.initjs()
df_cluster_scaled = pd.DataFrame(pipe['scaler'].fit_transform(X), columns=X.columns)
explainer = shap.TreeExplainer(model=pipe['RF'])
shap_values = explainer.shap_values(X=df_cluster_scaled)
shap.summary_plot(shap_values[0], df_cluster_scaled, plot_type="bar", show=False)
plt.savefig('iris_073_feature_inportance_shap.png')
plt.show()
確認
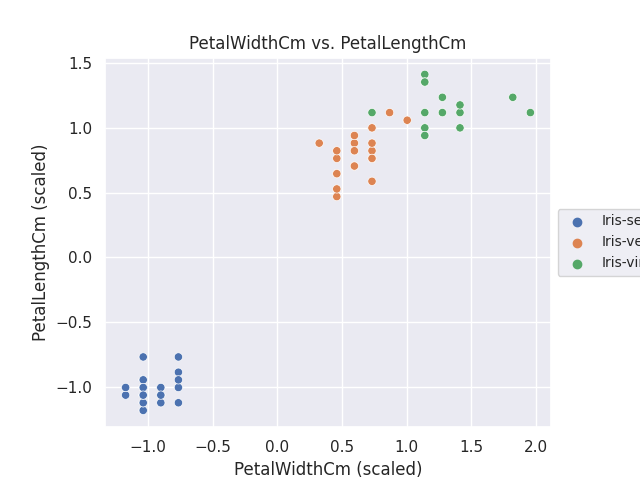
今回は少量のデータをサンプルに使ったためか、特徴量の重要度の算出はどのやり方でも似たような結果になりました。最後の SHAP による特徴量のインパクトから上位2つの特徴量について、クラスタに分類したデータ(標準化済み)を散布図にしました。
import numpy as np
feature_names = X.columns
result = pd.DataFrame(shap_values[0], columns=feature_names)
vals = np.abs(result.values).mean(0)
shap_importance = pd.DataFrame(
list(zip(feature_names, vals)),
columns=['feature name','feature importance']
)
shap_importance.sort_values(
by=['feature importance'],
ascending=False,
inplace=True
)
dfi.export(shap_importance, 'table_075_importances_shap.png')
shap_importance
data_x = shap_importance.iloc[0, 0]
data_y = shap_importance.iloc[1, 0]
fig, ax = plt.subplots()
sns.scatterplot(data=df_cluster_scaled, x=data_x, y=data_y, hue=list(df_cluster['Species']), ax=ax)
ax.set_aspect('equal')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5), fontsize=10)
ax.set_title('%s vs. %s' % (data_x, data_y))
ax.set_xlabel('%s (scaled)' % data_x)
ax.set_ylabel('%s (scaled)' % data_y)
plt.savefig('iris_076_top_2_importances.png')
plt.show()
データ数が少なく、特徴量の数も少ないので、わざわざ主成分分析をするまでもない冴えない結果になってしまいました。😅
機械学習というと、予測モデルを作って、その精度が云々という利用が多いのかもしれませんが、自分の場合、多変量解析でこのように分類されたモデルから有意な特徴量を評価するニーズが多いので、備忘録としてまとめました。
参考サイト
- bitWalk's: 【備忘録】主成分分析 ~ Python / Scikit-Learn ~ [2022-12-27]
- Permutation Importance vs Random Forest Feature Importance (MDI)
- 決定木アルゴリズムの重要度(importance)を正しく解釈しよう │ キヨシの命題 [2019-09-16]
- Permutation Importanceを使ってモデルがどの特徴量から学習したかを定量化する | DataRobot [2019-06-13]
- SHAPを用いて機械学習モデルを説明する l DataRobot [2021-04-14]
にほんブログ村
#オープンソース