SciPy を利用した数値積分

SciPy は Python のための科学的ツールのオープンソース・ライブラリとして開発されています。SciPyは、NumPy をベースにしていて、統計、最適化、積分、線形代数、フーリエ変換、信号・イメージ処理、遺伝的アルゴリズム、ODE (常微分方程式) ソルバ、特殊関数、その他のモジュールを提供しています。

Wikipedia より引用、編集

時系列のトレンドデータを解析する際に、ある区間を数値積分して、その（符号付きの）面積を評価したい場合があります。こういう場合、その面積の精度はそこそこで良いし、面積の単位とかを問題にするわけでもないので、前提条件を決めて数値積分するルーチンを自前で作成して使っていましたが、SciPy に数値積分するパッケージがあるので利用してみました。

下記の OS 環境で動作確認をしています。

	RHEL 9.4	x86_64
	Python	3.12.1
	jupyterlab	4.2.3
	matplotlib	3.9.1
	numpy	2.0.0
	pandas	2.2.2
	scipy	1.14.0

サンプルデータ

今回使用するデモ用のサンプルは、気象庁の過去の気象データ・ダウンロード・サイト [1] からダウンロードした、東京における 2023 年の気温データです。利用しやすいように加工しました。下記に CSV ファイルをダウンロードできるようにしました。

2023_temp_data.csv

以下、JupyterLab で確認しています。

CSV データの読み込み

下記のようにして、CSV ファイルを Pandas のデータファイルとして読み込みます。

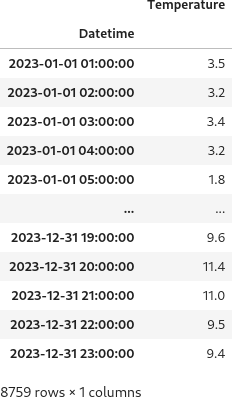
import pandas as pd   file = '2023_temp_data.csv' df = pd.read_csv(file, index_col=0, parse_dates=True) df

データフレームのインデックスに日時列を割り当てています。一時間毎の気温データです。

データの視覚化

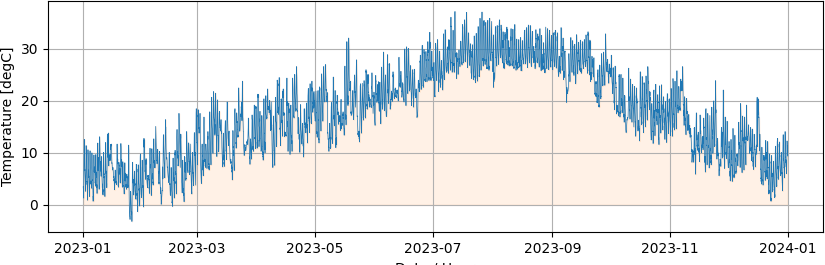
Matplotlib でデータを視覚化します。数値積分は下記プロットのオレンジ色の領域の（符号付き）面積を求めることになります。

import matplotlib.pyplot as plt   plt.rcParams["figure.figsize"] = (10,3) fig, ax = plt.subplots()   ax.plot(df, lw=0.5, c='C0') ax.fill_between(df.index, df['Temperature'], color='C1', alpha=0.1) ax.set_xlabel('Date / Hour') ax.set_ylabel('Temperature [degC]') ax.grid()   plt.savefig('temperature_002.png') plt.show()

積分する値の見積り

一年分の気温データですので、気温の平均値に一年 356 日を乗じてどの程度の量になるか見積もります。

import numpy as np   area_est = np.mean(df['Temperature']) * 365 print('mean * 365 days : %.3f' % area_est)

mean * 365 days : 6459.058

この計算だと大体 6000 台の数量です。平均値を使って算出したこの数量は、案外、積分する値の妥当な推定値になっているかもしれませんが…、とにかく数値積分をしてみましょう。

データフレームのデータは一時間毎のデータですので、数値積分した数量が、平均値と日数で見積もった数量と同程度のオーダーになるようにします。具体的には、日時を UNIX タイムスタンプ（秒）に変換し、これを 24 x 60 x 60 で割って、秒から日へ大きさを調整します。この数列を x とします。

y はもちろん気温データ列になります。

x = np.array([t.timestamp() / (24 * 60 * 60) for t in df.index]) y = np.array(df['Temperature'])

SciPy による数値積分

SciPy の integrate パッケージで利用できる、台形公式 (integrate.trapezoid)、シンプソンの公式 (integrate.simpson) それぞれの方法で数値積分をしました。

from scipy import integrate   area1 = integrate.trapezoid(y, x=x) print('Trapezoidal rule : %.3f' % area1)   area2 = integrate.simpson(y, x=x) print('Simpson\'s rule   : %.3f' % area2)

Trapezoidal rule : 6458.052
Simpson's rule   : 6458.646

今回の１万個に満たないデータ数では、台形公式とシンプソンの公式で計算時間に差異を感じませんでした。どちらの方法でも概ね同じ結果が出ていますが、用途によっては精度が必要な場合もあるでしょう。頻繁に利用する場合には、必要な精度と計算量（リソース）を評価して、どちらかに決める必要があります。

トップへ

参考サイト

1. 気象庁|過去の気象データ・ダウンロード
2. trapezoid — SciPy Manual
3. simpson — SciPy Manual

 

にほんブログ村


#オープンソース