Statsmodels は、データの探索、統計モデルの推定、統計検定を算出できる Python パッケージです。様々なタイプのデータや各推定量に対して、広範な記述統計量,統計検定,プロット関数、そして(サンプルに利用できる)統計データを利用できます。SciPy パッケージの stats モジュールを補完します。
最近、思っているような時系列解析ができずに苦しんでいます。あれこれ試している中で、Python の statsmodels パッケージで Unobserved components models [1] を試して見たところ、大したチューニングもしていないのに、いかにももっともらしい予測が出たことに衝撃を受けたので、試したことを備忘録にしました。
下記の OS 環境で動作確認をしています。

|
Fedora Workstation 40 | x86_64 |
| Python | 3.12.2 | |
| jupyterlab | 4.1.8 | |
| matplotlib | 3.8.4 | |
| pandas | 2.2.2 | |
| statsmodels | 0.14.2 |
今回の解析は JupyterLab を使用しています。
必要なライブラリーの読み込み
最初に、必要なライブラリーを読み込んでおきます。またプロットに共通な設定もしておきます。
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.rcParams.update({
'font.size' : 14,
'axes.grid' : True,
'grid.linestyle' : '--',
'figure.figsize' : [12, 6]
})
import statsmodels.datasets.co2 as co2
データセット
ちょうど参考サイト [2] で紹介されているサンプルを試していたので、そこで使用していたデータセットと同じく statsmodels に用意されている CO2 濃度のデータセットを利用して、同じように加工します。
co2_raw = co2.load().data co2_raw
欠損が少ない 1965 年以降のデータから月次平均を算出して使用します。
df = co2_raw.loc['1965-01-01':]
df = df.resample('ME').mean() # 月の最終日で月次データに変換
df.index.name = "YEAR"
df
集計したデータをプロットします。
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(df)
ax.set_title('CO2 Concentration')
ax.set_xlabel('Year')
ax.set_ylabel('ppmv')
# plt.savefig('trend_analysis_08/fig-001.png')
plt.show()
Unobserved components モデル
ここからは、参考サイト [3] で紹介されているやり方を、加工した CO2 濃度のデータセットをあてはめてみます。
※「空間状態モデル」というべきかもしれませんが、まだ全然理解できていないので知ったかぶりができず、さりとて、Unobserved components について(定着しているような)日本語の訳語を確認できなかったので、控えめに、そのままの表記にしています。
最初にモデルを定義して、(カルマンフィルダーで)フィッティングします。
model = sm.tsa.UnobservedComponents(
df,
level='local linear trend',
seasonal=12,
)
results = model.fit()
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 4 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 3.80232D+00 |proj g|= 8.88849D-02
At iterate 5 f= 2.31489D+00 |proj g|= 8.31771D-01
ys=-1.847E+00 -gs= 2.050E-01 BFGS update SKIPPED
At iterate 10 f= 4.99810D-01 |proj g|= 1.27619D+00
This problem is unconstrained.
At iterate 15 f= 3.45421D-01 |proj g|= 3.76042D-01
At iterate 20 f= 2.46012D-01 |proj g|= 8.57193D-02
At iterate 25 f= 2.45718D-01 |proj g|= 1.68724D-02
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
4 27 76 1 1 0 3.247D-03 2.457D-01
F = 0.24571746957084589
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
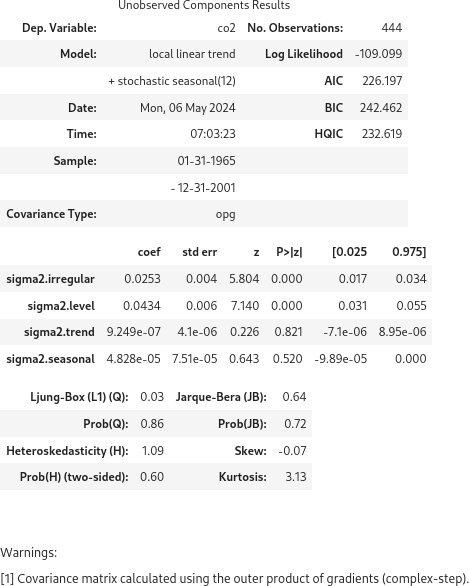
フィッティング結果のサマリーを表示できますが、経験不足で詳細を評価できません。
results.summary()
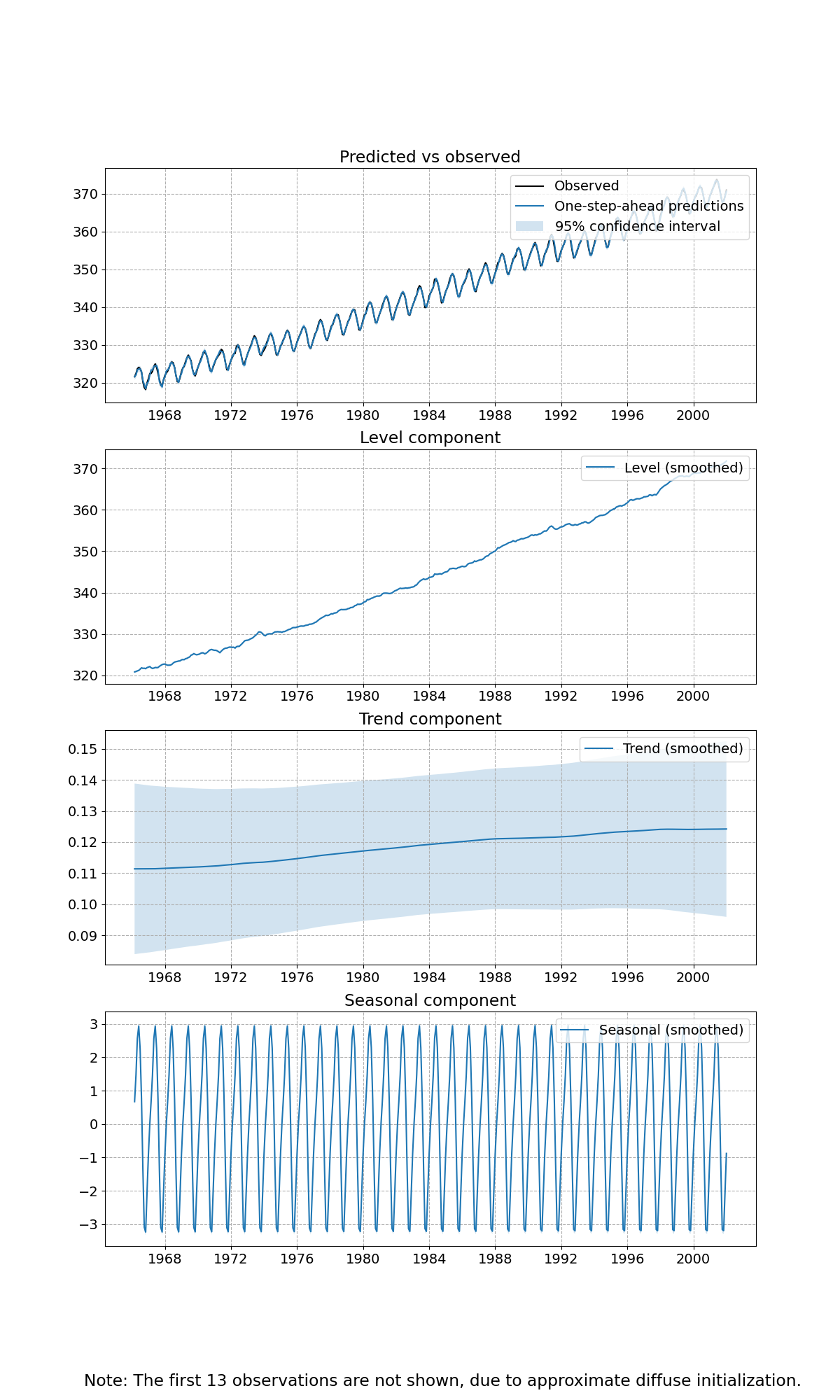
解析で分離した成分のプロットをします。
out = results.plot_components(figsize=(12, 20))
# plt.savefig('trend_analysis_08/fig-002.png')
1つ目のグラフは、観測値と予測値とその95%信頼区間を表しています。2つ目のグラフは、レベル成分(観測できない状態?)、3つ目のグラフは、トレンド成分とその信頼区間、4つ目のグラフは、季節成分(周期的変動)を表しています。
作成したモデルで未来を予測してみます。敢えて、一部の期間を学習データと予測データが重なるように設定しています。
# Prediction
prediction = results.predict('2000-01-31', '2005-12-31')
学習データ (Original) と予測データ (Predicted) を色を変えてプロットします。
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(df, label='Original', color="C0")
ax.plot(prediction, label='Predicted', color="C1")
ax.set_title('CO2 Concentration')
ax.set_xlabel('Year')
ax.set_ylabel('ppmv')
ax.legend()
# plt.savefig('trend_analysis_08/fig-003.png')
plt.show()
学習データとテストデータを分けてモデルの予測精度を検証していませんが、なんとなく自然な予測ができているように見えます。あくまで視覚的な印象に過ぎません。もしかすると CO2 濃度は、周期的な変化を把握しておけば素直に上昇を予測できるのかもしれません。
まとめ
今回使ったデータセットではたまたま季節性(周期的な変動)をうまく表現できただけかもしれません。それに、実際に解析したいデータにはこれほど強い季節性がないので、自分がやりたい時系列解析では、このモデルをそれほど有望視する必要がないかもしれません。しかし、参考サイト [4] を読んで、「外生変数」とよばれる、時間によって変化しない情報を複数加えられることを知り、俄然もっと使ってみたくなりました。
参考サイト
- statsmodels.tsa.statespace.structural.UnobservedComponents - statsmodels
- Pythonで時系列予測に使える機械学習モデルの実行例まとめ #Python - Qiita [2023-09-19]
- 時系列解析の重要手法、状態空間モデルについて解説 | pipon AI Trend 最新AI情報をわかりやすく届けるメディア [2020-04-29]
- Pythonで時系列分析(状態空間モデル) - deepblue [2022-10-12]
にほんブログ村
#オープンソース





0 件のコメント:
コメントを投稿