R による機械学習について、実例を用いた説明がされているサイトをいろいろ探しているなかで、R のパッケージ caret (Classification And REgression Training) を使った例を紹介している参考サイト に大変興味を持ちました。このサイトで紹介されている機械学習による予測モデルの作成は、自分が取り組んでいる多変量解析の業務に応用できる大変有用な情報だったからです。
より大きなサイズのデータに機械学習のアルゴリズムを適用して、一定の成果が得られたので、自分の理解を整理するために本ブログにその内容をまとめました。サンプルデータは、公開できるように値を標準化、変数名を変更するなどの加工を施してあります。
課題
ここで解析しようとすることを「課題」として表現すれば、以下のようになります。また使用するデータセット DATASET.csv を圧縮したファイルのリンク先も示しました。
ある製品の一製造工程において、処理中に取得できる製造装置のセンサー情報 (X1, X2, …, X233) を用いて、処理後に測定する特性 Y の値を処理装置毎 (A, B, C, D) および装置全体で予測せよ。ただし使用するデータセットは、下記 DATASET.zip をダウンロードして展開した DATASET.csv を用い、予測対象は処理日 (Date.Time) が 6 月 1 日以降のデータとする。
なお、処理装置 (Tool) は同じ構成で A, B, C, D の 4 台があり、処理数による特性 Y の値に変化のあることが経験的に判っているため、処理カウントを Count として含めている。
R スクリプト
まず、本記事で使用したスクリプトを以下に示しました。やや長くなるので、縦スクロールバーを付けて表示領域を節約しています。見返してみるとスマートでない処理が散見されますがご容赦ください。
library(tidyr)
library(dplyr)
library(caret)
library(ggpubr)
library(doParallel)
model.method <- "pls"
cl <- makePSOCKcluster(detectCores())
registerDoParallel(cl)
file.csv <- "/home/bitwalk/ドキュメント/ML_Test/DATASET.csv"
date.boundary <- as.POSIXlt("2018-06-01 00:00:00")
date.latest <- as.POSIXlt("2018-08-16 00:00:00")
target <- 0;
lcl <- -1;
ucl <- 1;
col.prd1 <- "#A0A0FF"
col.prd2 <- "#0000FF"
col.mea1 <- "#FFA0A0"
col.mea2 <- "#FF0000"
col.control <- "Dark Orange"
col.target <- "Dark Gray"
calc.performance <- function(df, pred, label) {
df[df$Tool == label, "n"] <- nrow(pred)
reg <- lm(Measured ~ Predicted, data = pred)
df[df$Tool == label, "RsqAdj"] <- sprintf("%5.1f", summary(reg)$adj.r.squared * 100)
df[df$Tool == label, "RMSE"] <- sprintf("%5.3f", sqrt(sum(pred$Delta * pred$Delta) / nrow(pred)))
TP <- nrow(pred[pred$TP == TRUE,])
TN <- nrow(pred[pred$TN == TRUE,])
FP <- nrow(pred[pred$FP == TRUE,])
FN <- nrow(pred[pred$FN == TRUE,])
df[df$Tool == label, "TP"] <- TP
df[df$Tool == label, "TN"] <- TN
df[df$Tool == label, "FP"] <- FP
df[df$Tool == label, "FN"] <- FN
df[df$Tool == label, "TPR"] <- sprintf("%5.1f", TP / (TP + FN) * 100)
df[df$Tool == label, "TNR"] <- sprintf("%5.1f", TN / (TN + FP) * 100)
df[df$Tool == label, "ACC"] <- sprintf("%5.1f", (TP + TN) / (TP + TN + FP + FN) * 100)
return(df)
}
get.name.model <- function() {
return(paste(dirname(file.csv),
paste0(name.metrology, "_", model.method, ".rds"),
sep="/"))
}
make.title <- function(prefix, metrology, name.method) {
label.method <- switch(name.method,
"bridge" = "Bayesian Ridge Regression",
"pls" = "PLS Regression",
"nnet" = "Neural Network",
"rf" = "Random Forest",
"xgbLinear" = "Gradient Boosting Linear",
"xgbTree" = "Gradient Boosting Tree",
stop("Enter something that switches me!")
)
return (paste(prefix, metrology, "by", label.method))
}
model.train <- function(df, name.method) {
gc()
set.seed(0)
model <- train(
Y ~ .,
data = df,
method = name.method,
tuneLength = 10,
preProcess = c('center', 'scale'),
trControl = trainControl(method = "cv")
)
return(model)
}
plot.corr.tools <- function(df, model.train, title.panel) {
df.tool <- data.frame(Tool = df$Tool,
Data = df$Y,
Predict = predict(model.train, df[, 1:(ncol(df) - 1)]))
d.min <- min(df.tool[, c("Data", "Predict")])
d.max <- max(df.tool[, c("Data", "Predict")])
range.axis <- c(d.min, d.max)
p1 <- plot.correlation(df.tool[df.tool$Tool == "A", ], "A", range.axis)
p2 <- plot.correlation(df.tool[df.tool$Tool == "B", ], "B", range.axis)
p3 <- plot.correlation(df.tool[df.tool$Tool == "C", ], "C", range.axis)
p4 <- plot.correlation(df.tool[df.tool$Tool == "D", ], "D", range.axis)
figure <- ggarrange(p1, p2, p3, p4, ncol = 2, nrow = 2)
annotate_figure(figure,
top = text_grob(title.panel, color = "black", face = "bold", size = 14),
bottom = text_grob("Measured Y", color = "black", face = "plain", size = 14),
left = text_grob("Predicted Y", color = "black", face = "plain", size = 14, rot = 90))
}
plot.correlation <- function(df, pm, limit) {
p <- ggscatter(df, x = "Data", y = "Predict",
xlim = limit, ylim = limit, color = 'magenta',
add = "reg.line",
add.params = list(color = "blue", fill = "lightblue"),
conf.int = TRUE, conf.int.level = 0.95, cor.coef = TRUE, cor.method = "pearson",
main = pm,
xlab = "", ylab = "")
return(p)
}
plot.trend.meas.pred <- function(df, name.tool, limit.x, limit.y) {
plot(df$Date.Time, df$Predicted, type = "n",
main = name.tool,
xaxt = "n", xlim = limit.x, xlab = "Date",
ylim = limit.y, ylab = "Y")
x.tick <- seq(as.POSIXct(limit.x[1], origin = "1970-01-01"),
as.POSIXct(limit.x[2], origin = "1970-01-01"),
by="1 week")
axis.POSIXct(side = 1, at = x.tick, format = "%m/%d")
abline(v = x.tick, lty = 3, col = "lightgray")
grid(nx = NULL, ny = NULL, col = "lightgray", lty = "dotted")
Map(function(x1, x2, x3)
axis(side = 4, at = x1, col.axis = x2, col.ticks = x2, labels = x3, lwd = 1, las = 1),
c(lcl, target, ucl),
c(col.control, col.target, col.control),
c("LCL", "Target", "UCL")
)
abline(h = target, lty = 1, col = col.target)
abline(h = lcl, lty = 3, col = col.control)
abline(h = ucl, lty = 3, col = col.control)
loop <- 1:nrow(df)
for (i in loop) {
x <- df[i, "Date.Time"]
y1 <- df[i, "Predicted"]
y2 <- df[i, "Measured"]
lines(c(x, x), c(y1, y2), col = "gray")
if ((lcl <= y1) && (y1 <= ucl)) {
col.pred = col.prd1
} else {
col.pred = col.prd2
}
points(x, y1, col = col.pred, pch = 16, cex = 1.2)
if ((lcl <= y2) && (y2 <= ucl)) {
col.meas = col.mea1
} else {
col.meas = col.mea2
}
points(x, y2, col = col.meas, pch = 16, cex = 1.2)
}
}
data <- read.csv(file.csv, header = T, row.names = NULL, as.is = T)
name.metrology <- names(data)[ncol(data)]
names(data)[ncol(data)] <- "Y"
data$Date.Time <- as.POSIXlt(data$Date.Time)
data$Tool <- as.factor(data$Tool)
data.train <- data[data$Date.Time < date.boundary, names(data) != "Date.Time"]
data.test <- data[data$Date.Time >= date.boundary, names(data) != "Date.Time"]
name.model <- get.name.model()
flag.model <- FALSE
if (file.exists(name.model)) {
modelTrained <- readRDS(name.model)
flag.model <- TRUE
} else {
modelTrained <- model.train(data.train, model.method)
}
modelTrained
plot.corr.tools(data.train, modelTrained, make.title("Training", name.metrology, model.method))
plot.corr.tools(data.test, modelTrained, make.title("Test", name.metrology, model.method))
flag <- data$Date.Time >= date.boundary
data.pred <- data.frame(Date.Time = data[flag, "Date.Time"],
Tool = data[flag, "Tool"],
Measured = data[flag, "Y"],
Predicted = predict(modelTrained, data.test[, 1:(ncol(data.test) - 1)]))
data.pred$Delta <- data.pred$Measured - data.pred$Predicted
data.pred$Target <- target
data.pred$LCL <- lcl
data.pred$UCL <- ucl
data.pred$TP <- ((data.pred$LCL > data.pred$Predicted) | (data.pred$Predicted > data.pred$UCL)) &
((data.pred$LCL > data.pred$Measured) | (data.pred$Measured > data.pred$UCL))
data.pred$TN <- ((data.pred$LCL <= data.pred$Predicted) & (data.pred$Predicted <= data.pred$UCL)) &
((data.pred$LCL <= data.pred$Measured) & (data.pred$Measured <= data.pred$UCL))
data.pred$FP <- ((data.pred$LCL > data.pred$Predicted) | (data.pred$Predicted > data.pred$UCL)) &
((data.pred$LCL <= data.pred$Measured) & (data.pred$Measured <= data.pred$UCL))
data.pred$FN <- ((data.pred$LCL <= data.pred$Predicted) & (data.pred$Predicted <= data.pred$UCL)) &
((data.pred$LCL > data.pred$Measured) | (data.pred$Measured > data.pred$UCL))
result <- data.frame(Tool = c(as.character((sort(unique(data.pred$Tool)))), "ALL"),
n = NA, RsqAdj = NA, RMSE = NA, TP = NA, TN = NA, FP = NA, FN = NA, TPR = NA, TNR = NA, ACC = NA)
result <- calc.performance(result, data.pred, "ALL")
default.par <- par(no.readonly = TRUE)
par(oma = c(0, 0, 2.5, 0), mar = c(0, 0, 0, 0))
m <- matrix(c(1, 2, 3, 4, 5, 5), nrow = 3, ncol = 2, byrow = TRUE)
layout(mat = m, heights = c(0.4, 0.4, 0.2))
limit.plot.x <- as.numeric(c(date.boundary, date.latest))
limit.plot.y <- c(min(c(data.pred$Measured, data.pred$Predicted)),
max(c(data.pred$Measured, data.pred$Predicted)))
for (tool in sort(unique(data.pred$Tool))) {
tbl.data <- data.pred[data.pred$Tool == tool,]
result <- calc.performance(result, tbl.data, tool)
par(mar = c(4, 4, 2, 4) + 0.1)
plot.trend.meas.pred(tbl.data, tool, limit.plot.x, limit.plot.y)
}
plot(1, type = "n", axes = FALSE, xlab = "", ylab = "")
legend(x = "top", inset = 0,
legend = c("Measured(In Control)", "Predicted(In Control)", "Measured(OOC)", "Predicted(OOC)"),
col = c(col.mea1, col.prd1, col.mea2, col.prd2),
lwd = 0, pch = 16, cex = 1, horiz = TRUE)
mtext(side = 3, line = 1, outer = T,
text = make.title("Test", name.metrology, model.method),
cex = 1.2, font = 2)
par(default.par)
print(model.method)
print(result)
if (!flag.model) {
saveRDS(modelTrained, file = name.model)
}
処理の流れ
処理の流れを、スクリプトから抜き取って説明します。
CPU のマルチコア/スレッド対応
計算時間を少しでも短縮させるために、CPU のマルチコア/スレッドに対応させるように次の処理をしています。
CPU のマルチコア/スレッド対応
library(doParallel)
cl <- makePSOCKcluster(detectCores())
registerDoParallel(cl)
データの構造
まずファイル DATASET.csv を以下のようにして読み込みます。黄色にマーキングした部分はお使いの環境に合わせて変更してください。
ファイルの読み込み
> file.csv <- "/home/bitwalk/ドキュメント/ML_Test/DATASET.csv"
> data <- read.csv(file.csv, header = T, row.names = NULL, as.is = T)
読み込んだデータフレーム data は以下のようになっています。先頭の列から Date.Time, Tool, Count と続き、装置センサーから得られた情報 X1, X2, …, X233 が続き、最後の列に計測した特性 Y の列があります。この例では、読み込んだ CSV ファイルの最後の列の列名は Y になっていますが、仮に別名であっても、スクリプトは最後の列の列名を強制的に Y に設定します。
CSV ファイルを読み込んだデータフレーム data の内容
> head(data)
Date.Time Tool Count X1 X2 X3 X4 X5 X6 X7
1 2015-05-25 23:55:00 B 7357 -0.01900170 -0.01900170 -0.0777002 -0.0777002 0.20459184 0.20459184 -0.000951094
2 2015-05-26 00:10:00 A 3896 -0.10106478 -0.10106478 -0.0690503 -0.0690503 0.32535613 0.32535613 0.180003453
3 2015-05-27 01:45:00 D 1536 -0.41100548 -0.41100548 -0.3285481 -0.3285481 -0.55801576 -0.55801576 -0.680284843
4 2015-05-27 02:16:00 C 7745 -0.33553069 -0.33553069 0.3720960 0.3720960 0.01976848 0.01976848 0.117837041
...
(途中省略)
...
X233 Y
1 -0.1409665 -0.09948111
2 0.3237569 -0.13414778
3 -0.1279232 0.52985222
4 0.4463080 -1.28081445
[ reached getOption("max.print") -- 2 行を無視しました ]
なお、Tool の列は、A, B, C, D からなる文字列ですので、念の為、因子化しています。しかし、因子化の有無で結果に違いが見られないので不要かもしれません。
Tool 列の因子化
> data$Tool <- as.factor(data$Tool)
> data$Tool
[1] B A D C C D C A A B B A B A C D B C D C B A D C C C C A D C C B C B C A D C C A B B C D C A B C D A B D C C D B
...
(途中省略)
...
[785] D C A B D A B C C A B A D C C B B A A B D C D C B A C D
Levels: A B C D
トレーニング・データとテスト・データの作成
読み込んだデータフレーム data を 2018 年 6 月 1 日より前と以降に分け、それぞれ、モデル生成のためのトレーニング・データ data.train と、予測し評価をおこなうためのテスト・データ data.test にします。なお、これらのデータでは時間情報は不要なので、最初の列 Date.Time を含めていません。
トレーニング・データとテスト・データの作成
> date.boundary <- as.POSIXlt("2018-06-01 00:00:00")
> data.train <- data[data$Date.Time < date.boundary, names(data) != "Date.Time"]
> data.test <- data[data$Date.Time >= date.boundary, names(data) != "Date.Time"]
ここで作成したトレーニング・データ data.train から Y を説明するモデルを、model.method で指定したアルゴリズムで生成します。次に、生成したモデルを使って、テスト・データ data.test にある変数から Y を予測し、 測定値である Y と比較し、そのパフォーマンスを評価します。
モデル生成のアルゴリズム
モデル生成は、PLS 回帰の方法をベースラインとして、機械学習のアルゴリズム Randome Forest と Gradient Boosting でどれだけの予測精度を持ったモデルを導き出すか、という観点で行っています。
ただ残念なことに、プライベートで使っている PC に搭載されている CPU が非力で、Gradient Boosting については計算に時間がかかりすぎるため割愛しました。
- Partial Least Square Regression(PLS 回帰)
- Random Forest
- Gradient Boosting / Linear
- Gradient Boosting / Tree
※ 業務では 12 コア / 24 スレッドの Xeon を搭載したサーバーを使用しているため、時間は掛ったものの 4 種類全ての方法を為すことができました。
R の caret パッケージでは、異なるモデル作成アルゴリズムでも同じ形式で処理させることができます。この例では次の形式でトレーニング・データからモデルを生成しています。
caret パッケージによるモデル生成
library(caret)
model.method <- "pls"
set.seed(0)
modelTrained <- train(
Y ~ .,
data = data.train,
method = model.method,
tuneLength = 10,
preProcess = c('center', 'scale'),
trControl = trainControl(method = "cv")
)
同じアルゴリズムで算出結果がいつも同じになるように set.seed(0) で同じ乱数値を与えるようにしていますが、必要がなければコメントアウトしてください。
生成されたモデルの保存
トレーニング・データを使って導き出したモデルは、アルゴリズムによっては算出にとても時間がかかるので、その都度計算するのではなく、保存して再利用できるようにしておけば効率的です。このスクリプトでは以下のようにして、読み込む CSV ファイルと同じディレクトリに、測定値の名前とアルゴリズム名を _ でつなげて、拡張子 .rds を付けて保存しています。
生成されたモデルの保存
> name.model <- paste(dirname(file.csv), paste0(name.metrology, "_", model.method, ".rds"), sep="/")
> saveRDS(modelTrained, file = name.model)
なお、スクリプトでは、対象のモデルが所定のディレクトリに保存されていれば、新たにモデルを生成せずに保存されているモデルを読み込んで予測を実施するようにしています。
生成されたモデルを使った予測
生成されたモデル modelTrained で、テスト・データ data.test の測定値 Y を予測するには次のようにします。
生成されたモデルによる予測
> predict(modelTrained, data.test)
[1] -0.564511093 -0.291840265 0.912656952 -0.184858401 -1.097866719 0.253638090 -0.837841432 0.086644599
[9] 0.256102807 0.021701389 -0.639044450 0.300414986 -0.889550871 -0.394218331 -1.467599951 0.586550660
[17] -0.420577535 -0.550688860 0.350506637 -0.517213392 0.060664828 -0.322848531 0.470435575 0.867269787
[25] 0.304300252 0.239735263 -0.351294722 -0.938820841 -1.363348925 0.290343418 -1.098006857 -0.246433971
[33] -0.026588716 0.391306218 -0.287707006 -0.397646853 -0.845069612 -0.509381204 -0.286503672 -0.947785809
[41] -0.544767030 -0.680410188 0.577058501 -0.230734517 -0.076479654 -1.196580077 -0.422268043 -0.997239284
[49] 0.185239426 -1.719159201 0.195633224 0.003232096 -0.393004324 0.102865151 -0.824430377 -0.923861202
[57] -0.097843073 -1.132868772 -0.699653500 -0.877830234 -0.290817663 -0.296070583 -0.832670460 -0.786971056
[65] -0.458646896 -0.996356577 -0.072015186 -1.377054543 -0.072389900 0.906125574 -0.318990203 -1.114962456
[73] 0.385677524 0.006426382 -0.031298885 -0.903859040 -0.465624144 0.095239571 -0.070603830 1.051526687
上記予測値と下記の実測値(測定値)との差を評価します。
測定値 Y
> data.test$Y
[1] 0.12118555 0.21518555 1.49985222 1.40851889 -1.19281445 0.17385222 -0.84881445 -0.00214778 0.72985222
[10] 1.00318555 -0.44614778 0.95918555 -0.35214778 0.43585222 -0.93081445 0.60651889 -0.04614778 0.38585222
[19] -0.39614778 -0.20214778 0.82651889 1.05918555 1.01518555 1.26785222 1.05585222 0.47985222 1.03518555
[28] -0.49614778 -0.53148111 1.17651889 -0.22548111 -0.11414778 0.39785222 1.27651889 0.83251889 -0.26681445
[37] -0.48414778 0.43585222 0.57385222 0.03918555 0.17385222 0.70318555 0.37118555 -0.08481445 0.19785222
[46] -1.05748111 -0.04614778 0.13318555 0.77118555 -0.76614778 0.51251889 0.30651889 0.21851889 0.17385222
[55] 0.74451889 -1.01348111 0.74718555 -0.04948111 -0.44014778 -0.81081445 0.09185222 0.52718555 -0.55481445
[64] -0.70748111 -0.70481445 -1.05748111 -0.26948111 -0.92814778 0.44185222 1.76118555 -0.22548111 -0.24348111
[73] 0.30318555 0.52985222 -0.70748111 -0.66081445 -0.61681445 1.09985222 0.04451889 0.34785222
予測と実測との差異の評価方法は用途によって異なると思いますが、ここではその一例を紹介します。
Partial Least Squares(PLS 回帰)
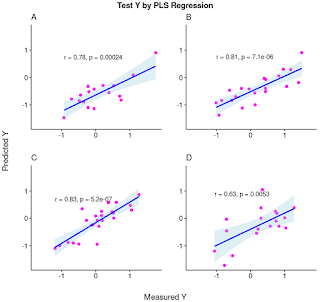
まず、ベースラインの PLS 回帰の結果を示しました。トレーニング・データ data.train、テスト・データ data.test それぞれ、測定値と予測値の相関を Tool 毎に確認しました。テスト・データの相関係数で、ざっくり +80% 程度あります。
PLS モデル : Correlation(Training と Test データセット)
テスト・データ test.data については、さらに時間を Date.Time を x 軸にとって、測定値(赤点)と予測値(青点)をプロットして、それぞれコントロールリミット (LCL, UCL) に入っているかに応じて色の濃淡を付けました。このケースでは、コントロール・リミット外れをどれだけ正確に予測できるかに興味があるので、コントロール・リミットを外れている点を濃い色にしています。
PLS モデル : Prediction(Test データセット)
予測パフォーマンスを評価する指標は、RsqAdj(R2 adjusted, 自由度調整済み決定係数)、RMSE (Root Mean Square Error)、および TPR (True Positive Rate, Hit Rate) としました。
RsqAdj (%) は大きければ大きいほど(100% まで)、相関が高いと評価できる指標ですが、ここでは参考指標に留めています。
RMSE は小さければ小さいほど良い予測と評価できる指標です。これを最重要の指標とみなしています。コントロール・リミット [-1, 1] をばらつきの ±3σ 相当とみなし、予測精度が 1σ = 1/3 = 0.33 以下を達成できることを期待しています。
TPR はこのケースでは、コントロールリミット外れを予測するモデルの正確さ(正答率)を表す指標です。実用的にはまず 50% 以上を達成できるモデルであることを期待しています。
PLS モデル : 予測パフォーマンス
> result
Tool n RsqAdj RMSE TP TN FP FN TPR TNR ACC
1 A 17 57.9 0.799 0 12 3 2 0.0 80.0 70.6
2 B 21 64.5 0.745 0 14 2 5 0.0 87.5 66.7
3 C 24 67.5 0.389 1 19 0 4 20.0 100.0 83.3
4 D 18 35.5 0.766 1 11 3 3 25.0 78.6 66.7
5 ALL 80 50.3 0.678 2 56 8 14 12.5 87.5 72.5
PLS を使って生成した予測モデルは Tool に依って差はあるものの、全体では RMSE が 0.678 と、目標の 0.33 の倍以上の値しか得られません。
Random Forest (RF)
Random Forest は機械学習のアルゴリズムのひとつで、分類、回帰、クラスタリングに用いられます。PLS と同じように予測モデルを生成しました。
PLS 回帰の時と同じようにして、トレーニング・データ data.train、テスト・データ data.test それぞれ、測定値と予測値の相関を Tool 毎に確認しました。トレーニング・データの相関については見た目でも PLS 回帰の場合よりばらつきが少く、+98% という高い相関係数が出ていますが、テスト・データでは Tool によって +70 〜 +90% とばらついています。トレーニング・データで高いフィッティングを得ることは、まず必要なことなのでしょうが、そのモデルで予測して確かに高い精度が得られるかどうかは、評価しなければわかりません。
Random Forest モデル : Correlation(Training と Test データセット)
同様にテスト・データ test.data のトレンドをプロットしました。
Random Forest モデル : Prediction(Test データセット)
予測モデルのパフォーマンスを以下にまとめました。
Random Forest モデル : 予測パフォーマンス
> result
Tool n RsqAdj RMSE TP TN FP FN TPR TNR ACC
1 A 17 44.7 0.615 0 15 0 2 0.0 100.0 88.2
2 B 21 70.7 0.689 0 16 0 5 0.0 100.0 76.2
3 C 24 61.8 0.407 0 19 0 5 0.0 100.0 79.2
4 D 18 82.5 0.441 0 14 0 4 0.0 100.0 77.8
5 ALL 80 58.0 0.547 0 64 0 16 0.0 100.0 80.0
この例では TPR が 0% になってしまいましたが、RMSE が 0.547 と、PLS 回帰の 0.678 と較べて小さい値が出ています。がしかし、これでも目標の 0.33 には届いていません。
まとめ
R の caret パッケージを利用すると、異なる機械学習のアルゴリズムを同じ形式で扱うことができます。caret パッケージに対する自分の理解度は、まだまだ使いこなせているレベルとは言えません。加えて原理的な理解も不十分なのですが、それでもいろいろなアルゴリズムを試して、パフォーマンスの違いを確認できるようになりました。ひとつ良い結果が出ると、その理由を理解するために必要な文献を求めるという良い循環が生まれています。
本稿では変数名を変更して値を標準化したり、コントロール・リミットを狭めたりといった加工を施してから、解析用のデータとして紹介していますので、実際のデータとは状況が少し違うのですが、実際のデータではパワフルなサーバーを使い、試したいアルゴリズムを全て試して、完璧とは言えませんが、そこそこ良い結果が得られています。この例では、測定値がこの工程の中でクローズしていますので、装置から得られるセンサーだけでどこまで現象を説明(予測)できるかに挑むことができますが、前工程の結果も影響している場合には、当然ですが事象はもっと複雑になります。
この手の予測技術について新たな手法や工夫の知見が得られれば、サンプルを準備して紹介していきたいと考えています。
参考サイト
- Rによる機械学習:caretパッケージの使い方 | Logics of Blue [2016-11-05]
- The caret Package: Documentation for the caret package
- Confusion matrix - Wikipedia
- 混同行列(Confusion Matrix)
 にほんブログ村
にほんブログ村