今回は一因子の実験で、水準が 3 以上の場合について、分散分析という手法を導入します。分散分析は、実験計画法において切っても切れない関係にあります。ここでは、概念的なことと R による計算例を紹介するに留め、分散分析の原理については詳しく立ち入っていません。
分散分析の必要性
1 因子の 2 水準の平均の違いを調べる方法が t 検定でした。それでは 3 水準(例えば A,B,C)になったらどうしたらよいでしょう。A と B、B と C、そして C と A のペアでそれぞれ t 検定を行ない、いずれかで帰無仮説が棄却されたならば、3 つの水準の平均は等しくない、と結論づけることができます。しかし、このやり方は水準 n の場合、 n * (n - 1) / 2 回の検定をしなければならず、効率的ではありません。
水準が 3 以上の場合には、因子の各水準の母平均に違いがあるかどうかを「分散」の大きさの違いで検定を行ないます。これを「分散分析 (Analysis of Variance, ANOVA)」といいます。複数の水準の平均が互いに等しいという帰無仮設を検定するもので,水準の間で少なくとも 1 つの平均が他と異なっているかどうかをこの分析では調べることになります。
一元配置分散分析
1 因子 1 つの効果を確認しようとする実験において、3 つ以上の水準で見る場合、上述のように分散分析を用いますが、これを一元配置分散分析 (one-way ANOVA) と呼びます。
| # | A社品 | B社品 | C社品 |
|---|---|---|---|
| 1 | 75.5 | 74.3 | 76.3 |
| 2 | 75.1 | 74.2 | 76.4 |
| 3 | 79.5 | 82.0 | 75.8 |
| 4 | 84.0 | 76.2 | 82.3 |
| 5 | 83.1 | 74.2 | 81.1 |
| 6 | 79.0 | 78.5 | 81.5 |
| 7 | 82.6 | 84.2 | 76.5 |
| 8 | 80.0 | 80.7 | 79.2 |
| 9 | 77.9 | 77.7 | 75.0 |
| 10 | 81.1 | 74.3 | 77.5 |
| 11 | 84.6 | 77.5 | 81.7 |
| 12 | 81.2 | 79.6 | 75.7 |
| 13 | 78.0 | 82.4 | 82.0 |
| 14 | 79.8 | 73.9 | 75.4 |
| 15 | 79.0 | 73.0 | 82.0 |
| 16 | 84.4 | 74.5 | 75.3 |
| 17 | 79.0 | 79.1 | 80.9 |
| 18 | 80.3 | 80.6 | 78.3 |
| 19 | 79.6 | 83.5 | 80.2 |
| 20 | 81.3 | 78.6 | 75.8 |
| 21 | 83.4 | 82.8 | 79.4 |
| 22 | 77.5 | 78.5 | 79.7 |
| 23 | 78.9 | 79.7 | 78.8 |
| 24 | 77.3 | 83.1 | 77.9 |
| 25 | 83.5 | 75.6 | 77.4 |
例)
ある製品の原料 W について、仕様が同じ 3 社の「A 社品」、「B 社品」、「C 社品」それぞれを使用した場合における収率の違いを評価したい。それぞれの原料を用いた 1 ロット、25 サンプルの収率の結果(右表)を用いて有意水準 5% で検定せよ。
帰無仮説 H0 は、『原料 W の水準「A 社品」、「B 社品」、「C 社品」では、収率に差は無い』になります。
まずは、右表のデータからデータフレームを作成します。
> a <- c(75.5, 75.1, 79.5, 84.0, 83.1, 79.0, 82.6, 80.0, 77.9, 81.1, 84.6, 81.2, 78.0, 79.8, 79.0, 84.4, 79.0, 80.3, 79.6, 81.3, 83.4, 77.5, 78.9, 77.3, 83.5) > b <- c(74.3, 74.2, 82.0, 76.2, 74.2, 78.5, 84.2, 80.7, 77.7, 74.3, 77.5, 79.6, 82.4, 73.9, 73.0, 74.5, 79.1, 80.6, 83.5, 78.6, 82.8, 78.5, 79.7, 83.1, 75.6) > c <- c(76.3, 76.4, 75.8, 82.3, 81.1, 81.5, 76.5, 79.2, 75.0, 77.5, 81.7, 75.7, 82.0, 75.4, 82.0, 75.3, 80.9, 78.3, 80.2, 75.8, 79.4, 79.7, 78.8, 77.9, 77.4) > y <- c(rep("A", 25), rep("B", 25), rep("C", 25)) > x <- c(rep("A", 25), rep("B", 25), rep("C", 25)) > tbl <- data.frame(原料W = x, 収率 = c(a, b, c)) > tbl 原料W 収率 1 A 75.5 2 A 75.1 3 A 79.5 ... (省略) ... 73 C 78.8 74 C 77.9 75 C 77.4 >
R の oneway.test() 関数を利用して一元配置分散分析をしてみましょう。このコマンドも t.test() 同様 、デフォルトではサンプルの等分散を仮定していない Welch の検定をするようになっていますので、var.euqal = T を指定して、サンプルが等分散であることを仮定します。
> oneway.test(収率 ~ 原料W, data = tbl, var.equal = TRUE)
One-way analysis of means
data: 収率 and 原料W
F = 3.2351, num df = 2, denom df = 72, p-value = 0.04515
有意水準 α = 0.05 の検定において、P-値 0.04515 は 0.05 よりも小さいので有意となり、材料W が収率に与える影響には差があると判断されます。
1 因子 3 水準実験
上の例を『ある製品の原料 W について、仕様が同じ 3 社の「A 社品」、「B 社品」、「C 社品」それぞれを使用した場合における収率の違いを評価するため、原料 W を因子とした 1 因子 3 水準の実験を計画し、右表の結果を得た。』と読みかえれば、(結果は変わらないものの)実験を計画/実施し、実験の解析をする問題に置き換わります。
分散分析モデルのあてはめをする aov() 関数(コマンド)と関連するコマンドを使って統計量を計算すると以下のようになります。
> result.aov <- aov(収率 ~ 原料W, data = tbl) > coefficients(result.aov) (Intercept) 原料WB 原料WC 80.224 -1.876 -1.740 > summary(result.aov) Df Sum Sq Mean Sq F value Pr(>F) 原料W 2 54.7 27.356 3.235 0.0451 * Residuals 72 608.8 8.456 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 > model.tables(result.aov) Tables of effects 原料W 原料W A B C 1.2053 -0.6707 -0.5347 > residuals(result.aov) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 -4.724 -5.124 -0.724 3.776 2.876 -1.224 2.376 -0.224 -2.324 0.876 4.376 0.976 -2.224 -0.424 -1.224 4.176 -1.224 0.076 -0.624 1.076 3.176 -2.724 -1.324 -2.924 3.276 -4.048 -4.148 3.652 -2.148 -4.148 0.152 5.852 2.352 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 -0.648 -4.048 -0.848 1.252 4.052 -4.448 -5.348 -3.848 0.752 2.252 5.152 0.252 4.452 0.152 1.352 4.752 -2.748 -2.184 -2.084 -2.684 3.816 2.616 3.016 -1.984 0.716 -3.484 -0.984 3.216 -2.784 3.516 -3.084 3.516 -3.184 67 68 69 70 71 72 73 74 75 2.416 -0.184 1.716 -2.684 0.916 1.216 0.316 -0.584 -1.084 >
分散分析では、水準の間で少なくとも 1 つの平均が他と異なっているかどうかを調べているにも関わらず、各水準の平均値が分析結果に出てこないので、tapply() 関数(コマンド)で、平均、分散、標準偏差を集計してみました。
> tapply(tbl$収率, tbl$原料W, mean) A B C 80.224 78.348 78.484 > tapply(tbl$収率, tbl$原料W, var) A B C 7.1144 12.1376 6.1164 > tapply(tbl$収率, tbl$原料W, sd) A B C 2.667283 3.483906 2.473136 >
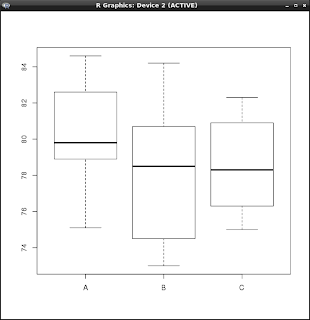
この手の分析では、データのばらつきは正規分布に従っていることを前提としていますが、現実のデータでは外れ値 (outlier) が平均値を引っ張っていることがありますので、ボックスプロット(箱ひげ図)で確認します。ボックスプロットは順序統計量を扱っています。
なお、この説明のために準備しているサンプルデータは一様乱数を使って生成していますので、正規分布に従わないばかりか、(十分なサンプル数があれば)外れ値もありません。
> bp <- boxplot(収率 ~ 原料W, data = tbl) > bp $stats [,1] [,2] [,3] [1,] 75.1 73.0 75.0 [2,] 78.9 74.5 76.3 [3,] 79.8 78.5 78.3 [4,] 82.6 80.7 80.9 [5,] 84.6 84.2 82.3 $n [1] 25 25 25 $conf [,1] [,2] [,3] [1,] 78.6308 76.5408 76.8464 [2,] 80.9692 80.4592 79.7536 $out numeric(0) $group numeric(0) $names [1] "A" "B" "C" >
参考文献
- 岩崎学 統計的データ解析入門 実験計画法 東京図書 (2006)


0 件のコメント:
コメントを投稿